Жадібний алгоритм - інтуїтивний та ефективний спосіб розв'язання задач оптимізації. І хоча його реалізація приваблює своєю очевидністю, він не завжди оптимальний. Необхідно точно розуміти, коли застосовувати жадібний підхід, а коли його варто уникати. В статті пропоную познайомитись з жадібними алгоритмами та потренуватись його застосовувати на задачі зі сайту codility.com.
Жадібний підхід
Жадібні алгоритми - це ціле сімейство алгоритмів (інколи ще говорять про жадібний підхід або жадібне програмування), тому немає якогось конкретного жадібного алгоритму, який можна закодувати. Проте, всі жадібні алгоритми побудовані згідно одного принципу - обирати оптимальне вирішення на кожному кроці, не зважаючи на кроки, які були зроблені до або будуть зроблені після. Іншими словами, жадібний алгоритм робить локально оптимальний вибір у сподіванні, що він приведе до глобально оптимального розв'язку.
Задача про монети
Розглянемо популярний приклад з монетками. Нехай у нас є монети номіналом 1, 2 і 5 копійок і нам необхідно відрахувати 10 копійок таким чином, щоб кількість монет була мінімальною.

За логікою жадібного підходу на кожному кроці необхідно обирати монету з найбільшим номіналом і це приведе до мінімальної їх кількості в результаті. Візьмемо 5 копійок, тепер можемо взяти ще одну монету в 5 копійок, не вийшовши за обмеження у 10. В результаті 10 коп. = 5 коп. + 5 коп. Кількість монет - 2 і це, дійсно, мінімально можлива їх кількість за даних умов.
Але якщо в задачу додати монету номіналом 6 копійок, це зробить застосування жадібного підходу не оптимальним. Дійсно, на першому кроці нам необхідно обрати 6, як монету з найбільшим номіналом, але далі ми не можемо обрати ні 6, ні 5, так як це перевищить ліміт у 10 копійок. Залишається дві монети по 2 коп. В результаті, ми маємо 10 як суму 6 + 2 + 2. В той час, як оптимальний розв'язок буде все ті ж 2 монети по 5.
В залежності від проблеми яку ми розв'язуємо, жадібний метод може бути оптимальним, а може і не бути. Якщо він дає не оптимальний розв'язок, часто, він дозволяє знайти рішення близьке до оптимального. В такому випадку необхідно скористатись іншим підходом, наприклад, повним перебором або динамічним програмуванням. Але, якщо жадібний підхід все ж працює коректно, час виконання алгоритму буде значно меншим за час виконання повного перебору чи при динамічному програмуванні.
Переваги і недоліки
-
Жадібний підхід легкий для розуміння і кодування. На кожному кроці алгоритму ми можемо абстрагуватись від попередніх і наступних кроків і думати лише про оптимальний розв'язок на даному етапі. Жадібний підхід не передбачає відміну вже зробленого вибору (повернення на попередні кроки) і не прогнозує нічого на майбутнє.
-
Швидкість виконання програми при жадібному підході легко передбачити, тому що складність алогритму очевидна. Найчастіше, вона лінійна, тобто, час виконання програми лінійно залежить від кількості вхідних даних. З іншими алгоритмічними підходами, такими як, наприклад, Розділяй і володарюй, це не завжди так.
-
Але у підходу є і великий недолік. У більшості випадків жадібний алгоритм працює некоректно. Необхідно дуже добре розуміти, коли його можна використовувати, а коли - ні. І навіть якщо жадібний алгоритм дає оптимальне вирішення в певних випадках, важко довести, що підхід буде працювати у всіх іншим можливих випадках.
В наведеному прикладі з монетами жадібний алгоритм добре працює для монет номіналом 1, 2, 5 але вже не працює для номіналів 1, 2, 5, 6. Варто зазаначити, що всі відомі мені грошові системи спроєктовані таким чином, що жадібний алгоритм працює для них коректно. Оскільки він простий і швидкий, люди легко знаходять потрібну суму для розрахунку в супермаркеті.
Правило застосування
Існує евристичне правило для розуміння застосовності жадібного підходу. Якщо обидві властивості наведені нижче справджуються, жадібний алгоритм може бути застосований до розв'язання задачі.
- Принцип жадібного вибору. Послідовність оптимальних виборів на кожному кроці приводить до оптимального рішення в кінці.
- Оптимальна підструктура. Задача має оптимальну підструктуру, якщо оптимальний розв'язок цілої задачі містить оптимальний розв'язок для будь якої підзадачі. Іншими словами, після заврешення певного кроку алгоритму залишається розв'язати задачу, для якої жадібний підхід також працює.
Спробуємо застосувати ці правила на прикладі Задачі про рюкзак.
Злодій проник на склад, де знаходяться три товари.
| Товар | Ціна | Вага |
|---|---|---|
| Товар А | 60 грн | 10 кг |
| Товар Б | 100 грн | 20 кг |
| Товар В | 120 грн | 30 кг |
Але у злодія є рюкзак лише на 50 кг. Яким чином він має вирішити, що взяти, щоб максимізувати свій прибуток?
Не важко побачити, що оптимальним рішенням буде взяти товари Б і В, що в сумі дасть 220 грн. Але, якби злодій застосував жадібний підхід, він би почав обирати товари з найбільшою питомою вартістю (відношенням ціни до ваги товару). Найдорожчим товаром є А, оскільки він коштує 6 грн/кг, тоді як Б і В коштують 5 і 4 грн/кг відповідно. Тобто, жадібний злодій обрав би товари А і Б, як найдорожчі і таким чином зміг би забрати з собою лише 160 грн, так як товар В вже не вліз би у рюкзак.
Повернемося до правила. Вибір першим товару А протирічить принципу жадібного відбору, адже не веде до оптимального рішення, яким є Б + В. Таким чином, жадібний алгоритм не може бути застосований в загальному випадку до Задачі про рюкзак.
Існує формальне доведення можливості або неможливості застосування жадібного алгоритму. Для цього необхідно звернутись до теорії Матроїдів. Якщо довести, що множина можливих розв'язків є матроїдом, згідно теореми Радо-Едмондса, до неї може бути успішно застосований жідібний підхід.
Використання на практиці
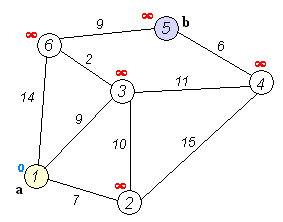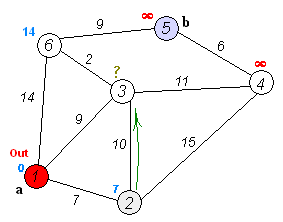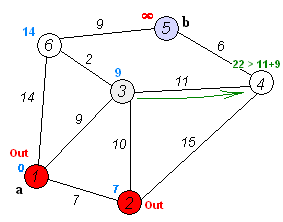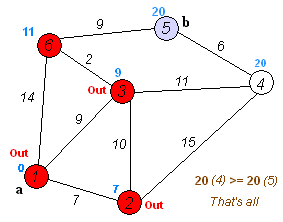
Жадібні алгоритми мають багато застосуваннь. Одним з найвідоміших є алгоритм Дейкстри для пошуку найкоротшого шляху у графі.
Алгоритм працює з невідвіданими вузлами і обчислює орієнтовну відстань від даного вузла до іншого. Якщо алгоритм знаходить коротший спосіб дістатися до заданого вузла, шлях оновлюється з урахуванням коротшої відстані. Ця задача має оптимальну підструктуру, оскільки, якщо вузел A пов'язаний з B, а B пов'язаний з C, і шлях повинен пройти через A і B, щоб дістатися до пункту призначення C, то найкоротший шлях від A до B і найкоротший шлях від B до C має бути частиною найкоротшого шляху від A до C. Таким чином, оптимальне рішення підзадачі приводить до оптимального вирішення вцілому.
Кодування Гаффмана - інший відомий приклад успішного застосування жадібного підходу. Алгоритм Гаффмана аналізує деякий текст і присвоює кожному символу код змінної довжини на основі частоти, з якою він зустрічається. Символи, що зустрічаються найчастіше будуть мати коротші коди, символи, що зустрічаються рідко будуть мати довгі коди. Таким чином можна значно зменшити (інколи до 80%) кількість інформації необхідної для передачі або зберігання тексту.
Задача про розклад також може бути розв'язана жадібно. Нехай у нас є кількість завдань, кожне з яких має певний дедлайн і винагороду. Виконання кожного завдання займає фіксований час. Винагорода буде виплачена, якщо завдання виконане до дедлайну. Необхідно обрати список завдань, щоб максимізувати свій прибуток.
Як бачимо, жадібний підхід може бути використаний в реальних задачах в різних областях, таких як складання розкладу, пошук оптимального шляху, кодування симолів та ін.
Задача з Codility
На сайті codility.com є досить багато матеріалів по алгоритмам і, що добре для нас, тестові задачі, які допоможуть закріпити знання.
Розв'яжемо задачу про відрізки, що не перетинаються, з уроку про жадібні алгоритми - MaxNonoverlappingSegments.
Отже, на координатній осі є відрізки, що задаються двома масивами A і B. Масив А містить координати початків, а B - координати кінців відрізків. Тобто, відрізок номер 1 починається в точці A[1] і закінчується в точці B[1].
Розглянемо такий приклад.
A[0] = 1 B[0] = 5
A[1] = 3 B[1] = 6
A[2] = 7 B[2] = 8
A[3] = 9 B[3] = 9
A[4] = 9 B[4] = 10
Відрізки показані на малюнку нижче.

Необхідно знайти максимальну кількість відрізків, які не перетинаються. Перетинаються ті відрізки, які мають хоча б одну спільну точку.
Для прикладу вище максимальною кількістю відрізків, що не перетинаються, є 3. Можливі варіанти: {0, 2, 3}, {0, 2, 4}, {1, 2, 3} або {1, 2, 4}. Якщо взяти будь які 4 відрізки, то хоча б два з них обов'язково перетнуться.
Задача містить додаткову умову, яка впливає на її розв'язання - відрізки відсортовані за координатою кінця. Іншими словами, масив B впорядкований по зростанню.
Почнемо зі створення проєкту xunit на C#.
> dotnet new xunit -n MaxNonoverlappingSegments
The template "xUnit Test Project" was created successfully.
Я обрав саме проєкт з юніт тестами, так як ми спробуємо написати спочатку тест і тільки потім реалізацію алгортиму.
Скопіюємо заготовку класу з сайту і самостійно створимо клас з тестом.
class Solution
{
public int solution(int[] A, int[] B)
{
throw new NotImplementedException();
}
}
public class UnitTest1
{
[Theory]
[InlineData(
new int[] { },
new int[] { },
0)]
public void Test(int[] a, int[] b, int result)
{
Assert.Equal(result, new Solution().solution(a, b));
}
}
Через атрибут InlineData задаються тестові дані. В даному випадку для порожнього списку очікується 0 відрізків, що не перетинаються.
Запустимо тест. Він завершився з помилкою NotImplementedException, адже клас Solution не реалізований. Давайте на першому етапі просто повернемо загальну кількість відрізків. Це повинно зпрацювати.
public int solution(int[] A, int[] B)
{
return A.Length;
}
Тепер тест завершився успішно.
Додамо також тест для одного відрізку і для двох відрізків, які не перетинаються.
[InlineData(
new int[] { 1 },
new int[] { 1 },
1)]
[InlineData(
new int[] { 1, 2 },
new int[] { 1, 3 },
2)]
Наш код все ще задовольняє цим тестам!
Але для ситуації двох відрізків, які перетинаються ([1, 2], [2, 3]), алгоритм вже не працює.
MaxNonoverlappingSegments.UnitTest1.Test(a: [1, 2], b: [2, 3], result: 1) [FAIL]
[xUnit.net 00:00:00.63] Assert.Equal() Failure
[xUnit.net 00:00:00.63] Expected: 1
[xUnit.net 00:00:00.63] Actual: 2
Тепер, власне, настав час реалізувати жадібний алгоритм вибору відрізків. Ідея, яка першою приходить в голову: рухаючись з права на ліво обирати перший доступний відрізок і запам'ятовувати його. Якщо наступний відрізок перетинається з поточним пропустимо його, якщо ж не перетинається, то збільшимо лічильник відрізків. Після цього необхідно запам'ятати наступний відрізок як поточний і рухатись далі.
Даний алгоритм можна застосувати, адже відрізки за умовою відсортовані за координатою кінця.
В коді це можна виразити наступним чином:
public int solution(int[] A, int[] B)
{
var result = 0;
var N = A.Length;
var position = int.MaxValue;
for (int i = N - 1; i >= 0; i--)
{
if (B[i] < position)
{
result++;
position = A[i];
}
}
return result;
}
Якщо бути точним, тут не запам'ятовується поточний відрізок, а лише координата його початку (змінна position), адже цього достатньо, щоб перевірити, чи наступний відрізок може бути включений у розв'язок. Якщо координата кінця поточного відрізку менша за position, він додається до результату і position змінюється на його початок.
Чудово, тепер всі тести пройдені! Додамо ще випадок описаний на сайті:
[InlineData(
new int[] { 1, 3, 7, 9, 9 },
new int[] { 5, 6, 8, 9, 10 },
3)]
Він теж завершується успішно, але не поспішаймо відправляти результат на перевірку. Наш алгоритм дозволяє зменшити проміжки між відрізками, але він не бере до уваги довжину відрізків. Якщо перший відрізок, який нам потрапить під руку, буде займати всю координатну вісь, алгоритм проігнорує всі інші відрізки. А серед них можуть бути декілька таких, що не перетинаються між собою. Тому наш алгоритм явно НЕ оптимальний. Цей тест описує такий випадок:
[InlineData(
new int[] { 1, 3, 1 },
new int[] { 2, 4, 5 },
3)]

Є три відрізки. Відрізок 1-5 найдовший і перекриває всі інші відрізки. Так як його кінець розташований найдалі, при жадібному підході він буде обраний першим і не дасть змоги включити інші відрізки в розв'язок. Замість правильного результату 2 (відрізки 1-2, 3-4) ми отримаємо в результаті 1 (відрізок 1-5).
Якщо ми відсортуємо відрізки по координаті початку і спробуємо йти від початку до кінця, то отримаємо ту ж саму проблему, але з іншого боку. Тому це не варіант.
Нам необхідно змінити функцію оптимальності, яка застосовується на кожному кроці. Якщо ми натрапили на відрізок, що коротший за поточний і все ще повністю ним перекривається, необхідно змінити поточний відрізок на більш короткий. Таким чином ми мінімізуємо довжину відрізків і максимізуємо їх кількість.
public int solution(int[] A, int[] B)
{
var result = 0;
var N = A.Length;
var position = int.MaxValue;
for (int i = N - 1; i >= 0; i--)
{
if (B[i] < position)
{
result++;
position = A[i];
continue;
}
if (A[i] > position)
{
position = A[i];
continue;
}
}
return result;
}
Перша частина алгоритму залишилась незмінною: якщо ми натрапляємо на відрізок, що може бути включений у розв'язок, інкрементуємо result і переходимо до наступного відрізку.
Якщо ми натрапили на відрізок, що повністю перекривається поточним (if (A[i] > position)), замінимо поточний відрізок на коротший.
Total tests: 6. Passed: 6. Failed: 0. Skipped: 0
Всі тести завершились успішно. Тепер можемо відправити даний код на перевірку.
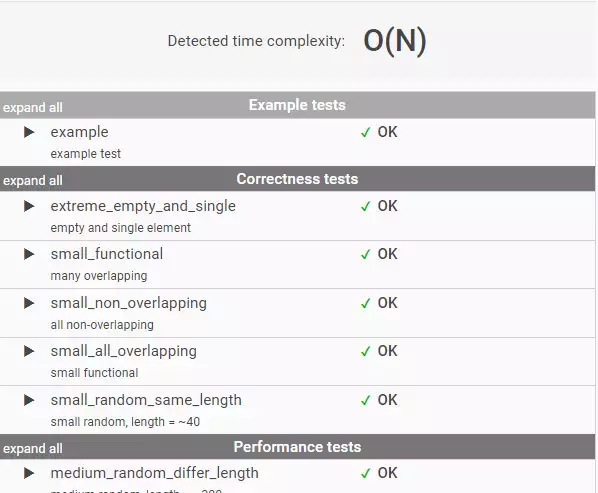
Як бачите, наш алгоритм не тільки коректний, він ще й оптимальний за часом. Його складність лінійна O(n).
Тестові приклади, які пропонує сайт codility.com не завжди покривають всі випадки, тому навіть якщо ваш код добре працює для пропонованих тестових даних спробуйте проаналізувати ваш розв'язок і уявити ситуації, в яких алгоритм може не спрацювати і створіть такі додаткові тести.
Висновок
Жадібний підхід - чудовий інтуїтивний і ефективний спосіб розв'язання багатьох популярних задач програмування. Його найбільшим недоліком є необхідність добре розуміти, коли він може бути застосований, а коли необхідно звернутись до іншого підходу. Але навіть в ситуаціях, коли жадібний алгоритм не дає оптимального рішення, його результат може бути близьким до оптимального і він точно буде ефективнішим за метод повного перебору або динамічне програмування.

Ще немає коментарів