Купа та черга з пріоритетом — ті структури даних, користь яких часто недооцінюється. Вони дозволяють легко та ефективно знайти найкращий елемент вибірки даних за певним критерієм. У Python з цими структурами можна працювати за допомогою модуля heapq, що є в стандартній бібліотеці. Модуль імплементує як низькорівневі, так і високорівневі операції над купою.
Черга з пріоритетом — потужний інструмент, який допомагає з найрізноманітнішими задачами: плануванням електронної пошти, пошуком найкоротшого маршруту на мапі, об'єднанням файлів з логуванням тощо. Загалом, працюючи над проєктами, ми щоденно стикаємось з проблемами оптимізації, де потрібно знайти найкращі елементи. Черга з пріоритетом та модуль heapq в Python допоможуть із цим.
У статті ми з'ясуємо:
- В чому сутність купи та черги з пріоритетом і як вони пов'язані.
- Які проблеми можна розв'язати за допомогою купи.
- Як використовувати модуль
heapq, аби отримати максимальну користь.
Цей матеріал призначений для пітоністів, які вже знайомі зі списками, словниками, сетами, генераторами та хочуть дослідити більш складні структури даних.
Структури даних
Купа — це конкретна структура даних, а черга з пріоритетом — абстрактна. Відмінність в тому, що абстрактні структури даних визначають інтерфейс, а конкретні відповідають за реалізацію.
Тож купа найчастіше використовується для реалізації черги з пріоритетом.
Конкретні структури даних дають певні гарантії продуктивності. Тобто зв'язок між обсягом даних та витраченим на обробку часом. Якщо розуміти це, то можна передбачити, як зміниться тривалість виконання програми, коли обсяг вхідних даних стане інакшим.
Купа та черга з пріоритетом
Як ми вже з'ясували, абстрактні структури даних визначають операції та відношення між ними. Черга з пріоритетом (як абстрактна структура даних) підтримує три операції:
-
is_emptyперевіряє, чи пуста черга; -
add_elementдодає елемент в чергу; -
pop_elementповертає елемент з найбільшим пріоритетом.
Чергу з пріоритетом часто використовують для оптимізації завдань, де метою є виконання таски з найбільшим пріоритетом. Коли завдання завершується, його пріоритет падає і воно повертається до черги.
Існує декілька угод для визначення пріоритетності елемента:
- Найбільші елементи мають найвищі пріоритети.
- І найменші елементи мають найвищі пріоритети.
Насправді це еквівалентні угоди, адже ви завжди можете змінити порядок пріоритетності елемента на протилежний. Наприклад, якщо ваші елементи — числа, то змініть знак числа — і ви зміните порядок пріоритетності.
Модуль heapq в Python дотримується другої угоди (найменший елемент — найпріоритетніший), яка є більш поширеною загалом. Далі ми розглянемо, як ця угода допомагає спростити ваш код.
Зверніть увагу: Модуль heapq в Python і структура даних купа не призначені для пошуку будь-якого елемента, окрім найменшого. Щоб знайти певний елемент за його розміром, найкраще скористатися бінарним деревом пошуку.
Конкретні структури даних реалізують операції, що визначені в абстрактних структурах даних, а також дають певні гарантії продуктивності.
Реалізації черги з пріоритетом за допомогою купи гарантує, що як додавання, так і видалення елемента виконуватимуться за логарифмічний час. Тобто час на ці операції буде зростати пропорційно до логарифма з основою 2 від кількості елементів.
Логарифми відрізняються відносно повільним зростанням. Логарифм з основою 2 від 15— це приблизно 4, а від трильйона — приблизно 40. Тобто якщо алгоритм досить швидкий для 15 елементів, то для трильйона елементів він буде лише в 10 разів повільнішим, а це досить гарний результат.
Якщо розглядати продуктивність алгоритму, варто пам'ятати, що абстрактні припущення щодо його швидкості менш важливі за справжні виміри конкретної програми та пошук вузьких місць. Але загальні припущення щодо продуктивності алгоритму все ж важливі для прогнозування поведінки програми. Пам'ятайте лише, що не всі прогнозування підтверджуються на практиці.
Реалізація купи
Як ми вже з'ясували, для реалізації черги з пріоритетом використовується купа. Розглянемо її структуру детальніше. Купа утворює повне бінарне дерево. У бінарному дереві кожен вузол має щонайбільше два нащадки. У повному бінарному дереві всі рівні, окрім найглибшого, завжди повинні мати два нащадки. Якщо найглибший вузол не повний, його вузли змістяться якнайдалі вліво.
Властивість завершеності гарантує, що глибина дерева є логарифмом з основою два від кількості елементів, округленого в більшу сторону. Розглянемо приклад завершеного бінарного дерева.
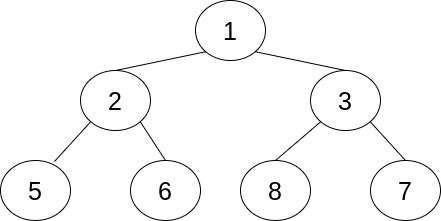
У двійковому дереві на зображенні всі рівні (крім останніх) завершені, тобто мають по два нащадки. Всього сім вузлів на трьох рівнях. Або ж логарифм з основою два від семи.
Вузол на найвищому рівні називається кореневим. Така назва може здатись нелогічною (корінь навряд чи асоціюється з верхівкою дерева). Однак така ієрархія добре ілюструє, що кількість порівнянь в купі — це логарифм з основою 2 від розміру дерева.
Зверніть увагу: порівняння іноді передбачає виклик користувацького коду за допомогою .lt(). Для Python це досить повільна операція, якщо порівняти з іншими операціями купи. Часто такі виклики провокують появу вузьких місць у продуктивності вашої програмі.
В купі значення поточного вузла завжди менше за значення обох його нащадків. Це властивість купи. Для порівняння, в бінарному дереві пошуку лише значення лівого вузла завжди повинно бути меншим за значення батьківського вузла.
Алгоритми вставки та видалення елемента з купи тимчасово порушують властивість купи. В цей час відбувається порівняння та переміщення вузла на потрібне місце.
Наприклад, для додавання елемента в купу, Python створює новий вузол на вільному місці. Якщо нижній шар структури не переповнений, то вузол додається знизу. В іншому випадку створюється новий рівень, куди додається новий елемент.
Далі Python порівнює новий вузол з батьківськими. Якщо властивість купи порушено, новий вузол та його батьківський вузол міняються місцями, тоді знов проводиться перевірка. Перевірки продовжуються доти, доки не буде поновлено властивість купи, або досягнуто верхівки дерева.
Подібний алгоритм використовується і для видалення найменшого елемента. Завдяки властивості купи ми знаємо, що цей елемент знаходиться на верхівці дерева.
Використання черги з пріоритетом
Черга з пріоритетом корисна для задач пошуку елемента, який має граничне значення певного критерію. Це можуть бути задачі:
- отримання найбільш популярного допису в блозі;
- пошук найшвидшого способу дістатися з однієї точки до іншої;
- прогнозування того, який автобус прибуде на зупинку швидше, враховуючи статистичні дані.
Планування електронної пошти — ще одне завдання, з яким допоможе впоратись черга з пріоритетом. Уявіть систему, де є декілька видів електронних листів, кожен з який надсилається з різною періодичністю. Один вид листів надсилається кожні 50 хвилин, інший — кожні 40.
Планувальник може додати обидва типи листів до черги і позначити час надсилання. Далі обирається елемент з найменшою міткою часу (тобто такий лист треба відправити наступним), розраховується час до надсилання. Планувальник оброблятиме відповідний лист, отримуючи його з черги пріоритетів, потім підраховуватиме наступний час надсилання та розміщуватиме лист в черзі заново, але вже на іншій позиції.
Купа в модулі heapq в Python
На початку статті ми з'ясували, що основою купи є бінарне дерево. Однак важливо пам'ятати одну деталь: це дерево має бути повним. Так ми завжди знаємо скільки елементів на кожному рівні, окрім останнього. Саме тому купу можна реалізувати в Python за допомогою списку (list). Така ж реалізація в модулі heapq в Python.
Для купи існує три правила, які визначають відношення між елементом з індексом k та елементами, що його оточують:
- Перший нащадок розташовний за індексом
2*k + 1. - Другий нащадок — за індексом
2*k + 2. - Індекс батьківського елемента визначається за формулою
(k - 1) // 2.
Зверніть увагу: символ // тут означає цілочисельне ділення. Тобто результат ділення завжди округлюється до цілого.
За допомогою цих правил список може зберігати бінарне дерево. Пам'ятайте, що в елемента завжди є батьківський елемент, а от дочірні елементи є не у всіх. Якщо індекс елемента 2*k за межами списку, то в такого елемента немає нащадків. Якщо індекс 2*k + 1 є в межах списку, а 2*k + 2 — ні, то в елемента є лише один нащадок.
Якщо позначити купу змінною h, то така властивість завжди буде правдивою:
h[k] <= h[2*k + 1] and h[k] <= h[2*k + 2]
Такий код може викликати помилку IndexError, якщо якийсь з індексів виявиться за межами списку, однак хибним такий вираз ніколи не буде.
Іншими словами, елемент завжди має бути меншим за елементи, що мають індекси 2*k + 1 та 2*k + 2.
Ось візуалізація цієї властивості:
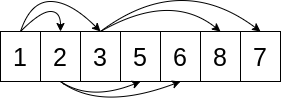
Стрілки направляються від елемента з індексом k до елементів з індексами 2*k + 1 та 2*k + 2. Наприклад, індексація елементів у списку в Python починається з нуля, тож стрілки вказуватимуть на елементи з індексами 1 та 2. Зверніть увагу, що стрілки завжди направлені від меншого значення до більшого. Тобто властивість купи справджується.
Базові операції
Модуль heapq в Python працює зі списками. На відміну від інших модулів, для цього він не оголошує власний клас, а пропонує функції, які працюють зі списками напряму.
Зазвичай елементи в купи розміщуються один біля одного. Особливо, якщо починати з пустої структури. Однак часто потрібно перетворити вже наявний список елементів в купу. Для цього в модулі heapq є функція heapify().
У цьому коді ми перетворюємо список на купу за допомогою heapify():
>>> import heapq
>>> a = [3, 5, 1, 2, 6, 8, 7]
>>> heapq.heapify(a)
>>> a
[1, 2, 3, 5, 6, 8, 7]
Хоч елемент 7 йде за елементом 8, список a досі дотримується властивості купи. Наприклад, елемент a[2] має значення 3, що менше за елемент a[2*2 + 2], тобто 7.
Як бачимо, heapify() одразу змінює список, але не сортує його. Купу не обов'язково сортувати, аби вона відповідала основній властивості. Та оскільки будь-який відсортований список задовольняє властивість купи, виклик heapify() для такого списку не змінить порядок його елементів.
Ще одна базова операція в модулі heapq, але вже для сформованої купи. Тут важливо зауважити, що пустий список або список з одного елемента завжди задовольняють властивість купи.
Оскільки кореневий елемент купи завжди перший в списку, вам не потрібна окрема функція для пошуку найменшого елемента. Просто зверніться до елемента за нульовим індексом.
Аби отримати найменший елемент з купи, зберігаючи її властивість, heapq пропонує heappop(). Поглянемо, як користуватися функцією:
>>> import heapq
>>> a = [1, 2, 3, 5, 6, 8, 7]
>>> heapq.heappop(a)
1
>>> a
[2, 5, 3, 7, 6, 8]
Функція повертає перший елемент, тобто 1, але при цьому зберігає свою властивість. Наприклад, елемент a[1] отримує значення 5, а елемент a[1*2 + 2] — 6.
Існує й обернена операція, heappush() — додавання елемента до купи, зберігаючи її властивість.
Розглянемо приклад:
>>> import heapq
>>> a = [2, 5, 3, 7, 6, 8]
>>> heapq.heappush(a, 4)
>>> a
[2, 5, 3, 7, 6, 8, 4]
>>> heapq.heappop(a)
2
>>> heapq.heappop(a)
3
>>> heapq.heappop(a)
4
Після додавання числа 4 до купи, ми дістаємо 3 елементи. Оскільки елементи 2 і 3 вже були в купі та були меншими за 4, їх отримуємо першими.
Ще декілька корисних операцій heapq:
-
heapreplace()— аналогічно доheappop(), за яким слідуєheappush(). -
heappushpop()— аналогічно доheappush(), за яким йдеheappop().
Такі операції корисні для деяких алгоритмів, оскільки вони більш продуктивні, аніж їхні альтернативи, викликані один за одним.
Високорівневі операції
Черга з пріоритетом часто використовується для об'єднання відсортованих послідовностей. Для таких цілей у модулі heapq є функція merge(). Вона очікує на вхід ітеровані відсортовані послідовності, які повертають ітератор, а не список.
Розглянемо функцію merge() для планування електронного листування.
import datetime
import heapq
def email(frequency, details):
current = datetime.datetime.now()
while True:
current += frequency
yield current, details
fast_email = email(datetime.timedelta(minutes=15), "fast email")
slow_email = email(datetime.timedelta(minutes=40), "slow email")
unified = heapq.merge(fast_email, slow_email)
На вхід функції merge() передаються нескінченні генератори. Функція повертає нескінченний ітератор і записує його в змінну unified. Ітератор видаватиме електронні листи для надсилання у порядку часових позначок.
Щоб переконатися, чи код виконався коректно, можна вивести перші 10 листів, що в черзі на відправлення:
>>> for _ in range(10):
... print(next(element))
(datetime.datetime(2020, 4, 12, 21, 27, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 21, 42, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 21, 52, 20, 305360), 'slow email')
(datetime.datetime(2020, 4, 12, 21, 57, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 22, 12, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 22, 27, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 22, 32, 20, 305360), 'slow email')
(datetime.datetime(2020, 4, 12, 22, 42, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 22, 57, 20, 305358), 'fast email')
(datetime.datetime(2020, 4, 12, 23, 12, 20, 305358), 'fast email')
Зверніть увагу, як надсилання листів з типом fast email планується кожні 15 хвилин, а для slow email — кожні 40 хвилин. Листи впорядковані відповідно до міток часу.
merge() не зчитує всі вхідні дані за раз, а робить це динамічно. Тому вивід перших 10 елементів відбувається досить швидко, хоча вхідні параметри і є нескінченними генераторами.
Навіть якщо вхідні дані досить об'ємні, процес займе помірний об'єм пам'яті. Це помітно при використанні merge для вже відсортованих послідовностей, відповідно до дати та часу (наприклад, для файлів логування).
Які проблеми розв'язує купа
Як ми вже з'ясували, купи чудово підходять для поступового об'єднання відсортованих послідовностей. Ми розглядали купу як структуру даних для реалізації застосунків планування періодичних завдань. Однак на цьому користь структури даних не закінчується.
Купа допоможе вам визначити перші або останні n-елементи за певним критерієм. Модуль heapq в Python також знадобиться.
Наприклад, в коді нижче обробляється вибірка результатів фіналу жіночого забігу на 100 метрів Олімпійських ігор 2016. Код виводить медалісток, тобто трьох учасниць з найкращим результатом.
>>> import heapq
>>> results="""\\
... Christania Williams 11.80
... Marie-Josee Ta Lou 10.86
... Elaine Thompson 10.71
... Tori Bowie 10.83
... Shelly-Ann Fraser-Pryce 10.86
... English Gardner 10.94
... Michelle-Lee Ahye 10.92
... Dafne Schippers 10.90
... """
>>> top_3 = heapq.nsmallest(
... 3, results.splitlines(), key=lambda x: float(x.split()[-1])
... )
>>> print("\
".join(top_3))
Elaine Thompson 10.71
Tori Bowie 10.83
Marie-Josee Ta Lou 10.86
Ми використали функцію nsmallest() з модуля heapq. Вона повертає найменші елементи в ітерованому об'єкті та приймає три аргументи:
-
n, тобто число елементів, які необхідно повернути; -
iterable, тобто елементи чи набір даних для порівняння; -
key— функцію, яка реалізовує логіку порівняння елементів.
Тут функція key розбиває рядки по символах пробілу, бере останній елемент та конвертує його у число з плаваючою комою. Далі відбувається сортування рядків за результатом забігу й повертаються три рядки з найменшим часом. Так визначаються три учасниці, які прибули найшвидше й отримали заслужену медаль.
В heapq також є функція nlargest(), яка приймає подібні параметри, але повертає протилежний результат.
Як класифікувати проблему
Купа — чудовий інструмент для виконання задач, де потрібно мати справу з граничними значеннями.
Вона може допомогти, якщо у вашій задачі є слова з цього списку:
- найбільший;
- найменший;
- найкращий;
- найгірший;
- верхній;
- нижній;
- максимальний;
- мінімальний;
- оптимальний.
Тож якщо потрібно знайти певний граничний елемент, варто звернути увагу на чергу з пріоритетом.
Іноді черга з пріоритетом — це лише частина розв'язку, коли потрібно додати ще й динамічного програмування. Далі ми розглянемо таку ситуацію на практиці — і ви зрозумієте, що динамічне програмування та черга з пріоритетами часто працюють в тандемі.
Приклад: пошук шляхів
У цьому прикладі реалізуємо задачу, близьку до тих, що трапляються в реальних застосунках, з використанням модуля heapq. Класичний алгоритм передбачає використання купи.
Уявіть, що є робот, який може переміщатись двомірним лабіринтом. Шлях необхідно почати з верхнього лівого боку, а дійти до призначення — в нижньому кутку праворуч. У робота є карта лабіринту в пам'яті, тож він може спланувати весь свій маршрут, перш ніж почати шлях.
Мета: дістатися фінішу лабіринту якнайшвидше.
Наш алгоритм — різновид алгоритму Дейкстри. Існує три структури даних, які оновлюються під час виконання алгоритму:
- карта орієнтовних шляхів від початку до позиції
pos. Шлях називається орієнтовним, тому що це найкоротший з відомих шляхів, однак пізніше ситуація може змінитись. - набір визначених точок, для яких карта орієнтовних шляхів показує найкоротший з можливих шляхів.
- купа позицій, що утворюють шлях, кандидатів. Ключ сортування купи є довжиною шляху.
На кожному кроці виконуються чотири дії:
- Отримується кандидат з купи.
- Кандидат додається до набору визначених точок. Якщо кандидат вже є в наборі, наступні дві дії пропускаються.
- Знаходиться найкоротший з відомих шляхів для поточного кандидата.
- Для кожного з прямих сусідів поточного кандидата проводиться перевірка: чи утворюють вони з кандидатом коротший шлях, аніж поточний орієнтовний шлях. Якщо це так, оновлюємо орієнтовний шлях і купу кандидатів новим шляхом.
Ці кроки виконуються циклічно, доки кінцева точка не потрапляє в набір визначених точок. На цьому алгоритм завершується. На виході отримуємо найкоротший з орієнтовних шляхів до точки призначення.
Початковий код
Тепер, коли ми крок за кроком розібрали алгоритм, час реалізувати його. Перш ніж перейти до імплементації кроків алгоритму, варто написати деякий допоміжний код.
Спершу імпортуємо модуль heapq:
import heapq
Функції heapq ми використовуватимемо для підтримки структури купи, щоб було простіше знайти позицію найкоротшого шляху на кожній ітерації.
Запишемо простір для пересування в змінну:
map = """\\
.......X..
.......X..
....XXXX..
..........
..........
"""
Тут мапа огорнута в triple-quoted рядок, що описує площину з перешкодами, якою може пересуватись робот.
Для демонстраційних цілей початкові дані ми записали в змінну. В реальних застосунках найімовірніше, що дані зчитуватимуться з файлу.
Мапа оголошена саме так, щоб бути зрозумілою людині, яка переглядатиме код. Позначки . показують допустимий простір для пересування, а X — перешкоди, через які робот пройти не може.
Допоміжний код
Створимо допоміжну функцію для конвертації мапи у структуру, яку буде простіше аналізувати в коді. parse_map() отримує мапу та аналізує її:
def parse_map(map):
lines = map.splitlines()
origin = 0, 0
destination = len(lines[-1]) - 1, len(lines) - 1
return lines, origin, destination
Функція приймає мапу і повертає кортеж з трьох елементів:
- Список рядків (
lines); - Початкову точку (
origin); - Точку призначення (
destination).
Тепер наш код зможе проаналізувати не лише людина, а й програма.
Перелік lines можна проіндексувати координатами (x, y). Вираз lines[y][x] повертає значення позиції. Можливі такі значення позиції:
- Крапка
.означатиме позицію у вільному просторі. - Літера
Xозначатиме позицію перешкоди.
Так можна визначити, яку позицію може зайняти робот.
Функція is_valid() визначає валідність позиції (x, y):
def is_valid(lines, position):
x, y = position
if not (0 <= y < len(lines) and 0 <= x < len(lines[y])):
return False
if lines[y][x] == "X":
return False
return True
Функція приймає два аргументи:
- перелік рядків
lines; - позицію, яку необхідно перевірити, у вигляді кортежу з двох координат
(x, y).
Аби бути валідною, позиція повинна бути у межах площини пересування, та не ставати перешкодою.
Наша функція перевіряє правильність координати y, звіривши її з довжиною списку lines. Щоб перевірити координату x, функція спочатку перевіряє, чи розташована вона всередині lines[y]. Тепер, коли відомо, що точка всередині доступної площини, перевіряється, чи це перешкода.
Ще одна корисна хелпер-функція, get_neighbors(), знаходить всі сусідні точки позиції:
def get_neighbors(lines, current):
x, y = current
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if dx == 0 and dy == 0:
continue
position = x + dx, y + dy
if is_valid(lines, position):
yield position
Функція повертає всі валідні позиції навколо поточної.
І наостанок: допоміжна функція get_shorter_paths() для пошуку коротшого шляху.
def get_shorter_paths(tentative, positions, through):
path = tentative[through] + [through]
for position in positions:
if position in tentative and len(tentative[position]) <= len(path):
continue
yield position, path
get_shorter_paths() повертає позиції з останнім кроком through. З ним шлях буде коротшим за поточний.
Функція приймає три параметри:
-
tentative— словник, який зіставляє позиції і найкоротший шлях, що їм відповідає; -
positions— ітерований об'єкт позицій, до яких ви хочете скоротити шлях; -
through— це позиція, після якої ви, можливо, знайдете коротший шлях доpositions.
Тут припускається, що до всіх елементів у positions можна дійти за один крок через through.
Функція get_shorter_paths() перевіряє, чи допоможе координата through зробити шлях до кожної з позицій коротшим. Якщо не було знайдено жодного шляху до позиції, тоді будь-який шлях вважатиметься коротшим. Якщо ж вже відомі шляхи, то функція поверне новий, лише якщо він коротший. Аби get_shorter_paths() була простішою у використанні, yield також повертає коротший шлях.
Всі допоміжні функції чисті, тобто вони не модифікують вхідні параметри, а створюють нове значення і повертають його. З ними написання основного алгоритму значно спроститься.
Програмуємо основний алгоритм
Нагадаємо, що наша мета — знайти найкоротший шлях між початковою точкою та призначенням.
Ми зберігаємо три структури даних:
- набір точних позицій в структурі сет;
- кандидати в структурі даних купа;
- орієнтовні шляхи зберігаються у словнику, де точки зіставляються з найкоротшим з відомих шляхів.
Позиція переходить до набору точних позицій, якщо ви впевнені, що вона формує найкоротший з можливих шляхів. Якщо точка призначення потрапляє в набір точних позицій, то найкоротший з відомих маршрутів до фінішу і є найкоротшим з можливих шляхів. Тобто мети алгоритму досягнуто.
Купа з точками-кандидатами candidates має довжину найкоротшого з відомих шляхів, а дії над нею здійснюються за допомогою функцій модуля heapq.
На кожному кроці ви розглядаєте точку-кандидата, яка формує найкоротший з відомих шляхів. Точка отримується з купи за допомогою heappop. До цієї точки немає коротшого шляху — всі інші шляхи проходять через інші вузли в candidates, і всі вони довші. Тож поточна точка-кандидат позначається як certain.
Далі ви перевіряєте її досі невідвіданих сусідів. Якщо після проходження через сусідню точку, ви отримаєте коротший шлях, вона додається до candidates за допомогою heappush().
Розглянемо функцію find_path(), яка реалізує цей алгоритм:
def find_path(map):
lines, origin, destination = parse_map(map)
tentative = {origin: []}
candidates = [(0, origin)]
certain = set()
while destination not in certain and len(candidates) > 0:
_ignored, current = heapq.heappop(candidates)
if current in certain:
continue
certain.add(current)
neighbors = set(get_neighbors(lines, current)) - certain
shorter = get_shorter_paths(tentative, neighbors, current)
for neighbor, path in shorter:
tentative[neighbor] = path
heapq.heappush(candidates, (len(path), neighbor))
if destination in tentative:
return tentative[destination] + [destination]
else:
raise ValueError("no path")
find_path() отримує мапу у вигляді рядка і повертає шлях від початку до фінішу у вигляді списку позицій.
Функція вийшла завеликою та складною, тому пояснимо її крок за кроком:
- Рядки 2–5: Визначаємо змінні, які оновлюватимуться в циклі. Для початку створюємо пустий шлях (з довжиною 0) від початку до фінішу.
-
Рядок 6: Визначає умову виходу з циклу. Якщо не залишилось точок в
candidates, то жоден шлях не можна скоротити. Якщоdestinationпотрапляє вcertain— те ж саме. - На рядках 7–10 ми отримуємо точку-кандидата за допомогою
heappop, пропускаючи цикл, якщо точка вже вcertain. В іншому випадку додаємо точку вcertain. Так ми можемо переконатись, що кожна точка-кандидат буде оброблена циклом хоча б один раз. - На рядках 11–15 викликаємо
get_neighbors()таget_shorter_paths(), аби знайти коротший шлях до сусідніх позицій і оновити словникtentativeта купуcandidates. - Рядки 16–19 відповідають за повернення правильного результату. Якщо найкоротший шлях знайдено, функція повертає його. Аби зробити API функції ще кориснішим, повернемо також кінцеву точку. Якщо функція не знайшла найкоротшого шляху, буде викликано виключення.
Так крок за кроком ми розібрали комплексну функцію на базові та зрозумілі кроки.
Трохи візуалізації
Якби нашим алгоритмом скористався робот, то йому було б зручніше працювати з переліком позицій, через які потрібно пройти. Аби результати алгоритму могла зрозуміти людина, варто їх візуалізувати.
Створимо функцію show_path(), яка покаже шлях на мапі:
def show_path(path, map):
lines = map.splitlines()
for x, y in path:
lines[y] = lines[y][:x] + "@" + lines[y][x + 1 :]
return "\
".join(lines) + "\
"
Функція приймає параметри path та map і повертає мапу з прокладеним шляхом за допомогою символів @.
Запускаємо код
Нам залишилось викликати реалізовані функції. Це легко зробити з інтерактивного інтерпретатора Python.
Ось результат роботи алгоритму:
>>> path = find_path(map)
>>> print(show_path(path, map))
@@.....X..
..@....X..
...@XXXX..
....@@@@@.
.........@
Тут ми отримуємо найкоротший шлях за допомогою find_path() та передаємо його в show_path(), аби візуалізувати результат.
Вітання! Ми виконали завдання, використовуючи модуль heapq в Python. Подібні задачі (що комбінують динамічні структури даних) часто трапляються на співбесідах та змаганнях. Наприклад, у 2019 році на Advent of Code була задача, яка розв'язувалась у схожий спосіб.
Підсумуємо
Матеріал має допомогти вам розібратись, що таке купа й черга з пріоритетом та який вид задач вони виконують. Ми також застосували модуль heapq на практиці та з'ясували, чим він корисний при роботі з купами.
Чому ми навчились:
- Використовувати низькорівневі функції модуля
heapqза допомогою купи чи черги з пріоритетом. - Застосовувати високорівневі функції модуля
heapqдля об'єднання відсортованих ітерованих об'єктів або пошуку найбільшого чи найменшого елементів. - Розпізнавати проблему, для розв'язку якої підходять купа чи черга з пріоритетом.
- Прогнозувати продуктивність коду, який використовує ці структури даних.
Сподіваємось, тепер ці знання допоможуть вам у багатьох щоденних задачах програмування.

Ще немає коментарів