Швидке піднесення до степеня

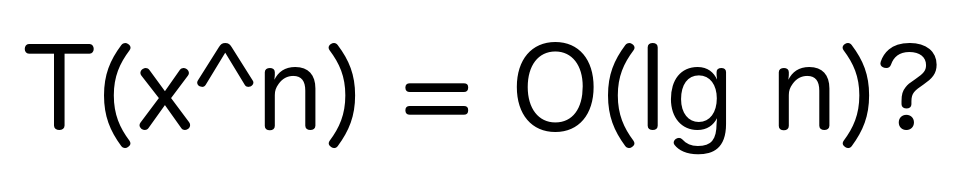
Розв'язуючи одну із задач на InterviewBit (шкода вже не пам'ятаю, яку саме), я побачив магічний (і мені невідомий) метод піднесення до степеня, який містив пропорційну логарифмічній кількість арифметичних операцій. Якщо відкинути магію, то метод дуже елегантний і зрозумілий.

Одразу код. Якщо все зрозуміло, то далі можна і не читати:

long pow(long val, long exp) {
    long res = 1;
    while(exp != 0) {
        if((exp & 1) == 1) res *= val;
        val *= val;
        exp >>= 1;
    }
    return res;
}

Конкретизуємо задачу: піднести x до степеня n, де x > 0 , n >= 0 і обидва цілі числа.

Якби мене запитали піднести щось до степеня, то я використав би найпростіший алгоритм, який випливає із визначення, і виконується за лінійний час.

Тобто:

x^n = x*x*x*....*x (n разів)

Прискіпливо вдивіться у формулу і спробуйте подумати, як можна зменшити кількість операцій множення. Хвилинка паузи. Можна побачити, що x*x це забагато разів повторювана операція. Якби ми використали додаткове число, скажімо y=x*x, то x^n = y*y*y*....*y*x або x^n = y*y*y*....*y*y в залежності від парності n. Припустимо, що ми вже знаємо y, тоді для вирахування x^n нам необхідно виконати вдвічі менше операцій множення. Точно за таким самим принципом ми могли б замінити y і ще зменшити кількість арфиметичних операцій, і часові затрати відповідно.

Тепер перейдомо питання реалізації. Для цього використаємо одну із властивістей степеня:

x^(a+b) = (x^a) * (x^b).

Отже для n=a+b, ми шукаємо випадок, коли a якимось чином пов'язана із b. Нас цікавить випадок, коли a=2*b, тоді x^a = x^b * x^b.

Використаємо те, що будь-яке число можна записати як суму степенів двійки, оскільки це фактично є записом числа у двійковій системі числення. Візьмемо число 177 за приклад:

117 = 64+32+16+4+1 = 2^6+2^5+2^4+2^2+2^0. 

Введемо у суму (із множником 0) степені двійки, яких немає в розкладанні числа:

117 = 1*2^6+1*2^5+1*2^4+0*2^3+1*2^2+0*2^1+1*2^0 = 1*e6+1*e5+1*e4+0*e3+1*e2+0*e1+1*e0,
e0=1 (2^0)
e1=2*e0 (2^1)
e2=2*e1 (2^2)
e3=2*e2 (2^3)
...
n[]=[1110101]
n[0]=1
n[1]=0
n[2]=1
...

Тоді:

x^117 = x^(n[6]*e6)*x^(n[5]*e5)*x^(n[4]*e4)*x^(n[3]*e3)*x^(n[2]*e2)*x^(n[1]*e1)*x^(n[0]*e0)

Узагальнимо:

x^n = mult(x^(n[i]*ei)) 
...
i=0..log(n), ei=2^i
x^e(i+1) = x^ei*x^ei

Запишемо словами: для того, щоб отримати x^n достатньо перемножити між собою усі x^(2^i), для яких значення біту під i рівне 1 ( i — номер розряду числа у двійковому записі числа n).

Для обрахунку наступного x^(2^i) нам потрібно тримати в пам'яті лише попереднє значення: x^(2^i) = x^(2^(i-1)) * x^(2^(i-1)). Такий підхід суттєво зменшує загальну кількість необхідних оперцій. Для прикладу: x^117 ми можемо отримати через 11 операцій множення, а не 117, як із використанням звичайного алгоритму.

І ще раз глянемо на код:

long pow(long x, long n) {
    long res = 1; //результат множення
    while(n != 0) {
        if((n & 1) == 1) res *= val; //x йде в результат
        x *= x; //x = x*x - для наступного розряду
        n >>= 1; //ділення на 2 методом побітового зсуву
    }
    return res;
}

П.С.

Звичайно, ми могли б використати будь-який інший формат запису замість двійкового, але зручність двійкового в тому, що числа, у більшості мов програмування, мають безкоштовну двійкову форму запису і зручні методи роботи із нею.

П.П.С.

Для великих чисал чималу кількість часу займає саме операція множення, тому алгоритм працюватиме суттєво довше на великих числах.