Стаття присвячена реалізації алгоритму Гауса для розв'язування системи лінійних алгебраїчних рівнянь на мові Java.
Теоретичні відомості
Розглянемо математичну теорію. Система лінійних рівнянь може мати рішення, нескінченно багато рішень або ж бути несумісною (не мати рішень). Не всі методи розв'язування СЛР можуть впоратись з другим випадком, коли система має нескінченно багато рішень. Наприклад, метод Крамера та матричний метод не застосовні, але метод Гауса цілком можна використовувати.
Алгоритм можна умовно розділити на два етапи:
- Прямий хід
- Зворотний хід
У першому етапі утворюються нулі нижче або вище головної діагоналі, коштом використання елементарних перетворень матриці. На другому етапі знаходять невідомі починаючи з кінця. Докладну теорію можна переглянути за посиланням: метод Гауса, тому з теорією, мабуть, все. Перейдемо до реалізації.
Реалізація
Почнемо з визначення завдання:
- Нам потрібно створити програму яка реалізую систему лінійних рівнянь у вигляді певної структури даних, використовуючи прийоми узагальненого програмування. Система повинна містити коефіцієнти похідного типу від класу Number (тобто Float, Integer, Double і т. д.)
- Запрограмувати алгоритм, який отримавши на вхід структуру даних системи утворює нулі нижче головної діагоналі
Почнемо з написання інтерфейсу, який має реалізовувати кожне рівняння:
package gaussa;
public interface Gaussa> {
public void addEquation(T item);
public void mul(N coefficient);
public N findCoefficient(N a, N b);
public N at(int index);
public int size();
}
Тут все повинно бути ясно, N деякий спадкоємець Number'a, T — деякий тип, що реалізує цей інтерфейс (рекурсивні дженерики). Метод addEquation(T item) дозволяє додати кожен елемент рівняння item до кожного свого члена. Інші методи працюють аналогічно.
Тепер розглянемо клас системи рівнянь. Як видно в лістингу нижче, він дженерелізований так само, як і інтерфейс Гауса і містить методи для зручного доступу до приватного списку містять у собі рівнянь.
package gaussa;
import java.util.ArrayList;
import java.util.List;
public class LinearSystem> {
private List list = new ArrayList();
public T get(int index){
return list.get(index);
}
public void push(T elem){
list.add(elem);
}
public int size(){
return list.size();
}
public N itemAt(int i, int j){
return list.get(i).at(j);
}
}
Тепер можна приступати до реалізації «окремого випадку» структури рівняння. Створимо клас MyEquation, що реалізує наш інтерфейс. Нехай спадкоємцем Number'а буде надточний клас Float (на практиці краще брати Double). Зверніть увагу, що в методі addEquation(MyEquation item) використовується об'єкт класу ListIterator, що дозволяє редагувати елементи списку що перебирається.
package gauss;
import java.util.ArrayList;
import java.util.List;
import java.util.ListIterator;
import java.util.Random;
public class MyEquation implements Gauss<Float, MyEquation> {
private List equation = new ArrayList();
public List getEquation(){
return equation;
}
public void generate(int size){
if (size < 2) size = 2;
this.equation.clear();
for (int i = 0; i < size; i++){
Random random = new Random();
this.equation.add((float) (random.nextInt()%10) + 1);
}
}
@Override
public int size(){
return equation.size();
}
@Override
public void addEquation(MyEquation item){
ListIterator i = equation.listIterator();
ListIterator j = item.getEquation().listIterator();
for(; i.hasNext() && j.hasNext();){
Float a = i.next();
Float b = j.next();
i.set(a + b);
}
}
@Override
public void mul(Float coefficient){
for(ListIterator i = equation.listIterator(); i.hasNext();){
Float next = i.next();
i.set(next * coefficient);
}
}
@Override
public Float findCoefficient(Float a, Float b){
if (a == 0.0f) return 1.0f;
return -b/a;
}
@Override
public Float at(int index){
return equation.get(index);
}
}
Тепер маємо повноцінну структуру даних, що реалізує систему рівнянь. Складемо алгоритм, який буде приймати деякий об'єкт, який реалізує інтерфейс Гауса, потім викликаючи потрібні методи призведе матрицю до потрібного вигляду.
package gauss;
public class Algorithm> {
LinearSystem<N, T> list = null;
public Algorithm(LinearSystem<N, T> system){
list = system;
}
public void calculate() throws NullPointerException, ArithmeticException{
if (list == null){
throw new NullPointerException("LinearSystem<N, T> instance equal null");
}
if (!checkSystem(list)){
throw new ArithmeticException("Incorrect system for Gauss Method");
}
for(int i = 0; i < list.size() - 1; i++){
for(int j = i + 1; j < list.size(); j++){
N k = list.get(j).findCoefficient(list.get(j).at(i), list.get(i).at(i));
list.get(j).mul(k);
list.get(j).addEquation(list.get(i));
}
}
}
private boolean checkSystem(LinearSystem<N, T> system){
if (system.size() < 2) return false;
for(int i = 0; i < system.size(); i++){
if (system.get(i).size() != (system.size() + 1)){
return false;
}
}
return true;
}
}
Алгоритм простий, знайти потрібний коефіцієнт, помножити на нього i-го рядка (i=0..n-1), і додати її до j-му рядку (j=i..n). Зауважте, алгоритм не знає як саме реалізуються методи findCoefficient, mul addEquation, це додає коду велику гнучкість, оскільки при потребі змінити способи маніпуляції рівняннями (рядками), будуть змінені тільки реалізації трьох вищезазначених методів, а головний алгоритм залишиться недоторканим.
Майже все. Залишилося запустити це все в методі main:
import gauss.Algorithm;
import gauss.MyEquation;
import gauss.LinearSystem;
public class Main {
private static final int DEFAULT_EQUATIONS_NUMBER = 2;
private static final int DEFAULT_VARIABLES_NUMBER = 2;
public static void main(String args[]){
LinearSystem<Float, MyEquation> list = generateSystem();
printSystem(list);
int i, j;
Algorithm<Float, MyEquation> alg = new Algorithm<Float, MyEquation>(list);
try{
alg.calculate();
}catch (NullPointerException e){
System.out.println(e.getMessage());
System.exit(0);
}catch (ArithmeticException e){
System.out.println(e.getMessage());
System.exit(0);
}
Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER];
for(i = list.size() - 1; i >= 0; i--) {
Float sum = 0.0f;
for(j = list.size() - 1; j > i; j--) {
sum += list.itemAt(i, j) * x[j];
}
x[i] = (list.itemAt(i, list.size()) - sum) / list.itemAt(i, j);
}
printSystem(list);
printVector(x);
}
public static LinearSystem<Float, MyEquation> generateSystem(){
LinearSystem<Float, MyEquation> list = new LinearSystem<Float, MyEquation>();
int i;
for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++){
MyEquation eq = new MyEquation();
eq.generate(DEFAULT_VARIABLES_NUMBER + 1);
list.push(eq);
}
return list;
}
public static void printSystem(LinearSystem<Float, MyEquation> system){
for (int i = 0; i < system.size(); i++){
MyEquation temp = system.get(i);
String s = "";
for (int j = 0; j < temp.size(); j++){
s += String.format("%f; %s", system.itemAt(i, j), "\t");
}
System.out.println(s);
}System.out.println("");
}
public static void printVector(Float [] x){
String s = "";
for (int i = 0; i < x.length; i++){
s += String.format("x%d = %f; ", i, x[i]);
}System.out.println(s);
}
}
Запустимо це диво, що б перевірити коректність роботи...
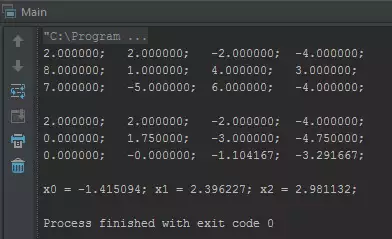 Це все. Вихідний код можна звантажити на github'e.
Це все. Вихідний код можна звантажити на github'e.
Висновок
Метод Гауса не дуже піддається узагальненого програмування (як бачите зворотний хід виконаний окремо), однак вийшла своєрідна реалізація яка, сподіваюся, допоможе кому то краще розібратися в мистецтві використання інтерфейсів і дженериків.

Коментарі (3)