Пропонуємо до вашої уваги серію статей, у яких ми розглянемо основи тригонометрії, зрозуміємо, чим вона може бути корисною та як творчо застосувати її у CSS та JavaScript. Розуміння тригонометрії може бути нам надзвичайно корисним, коли справа стосується творчого кодування. Але невтаємничених усе це може трохи лякати, тож спробуємо розібратись в цій темі.
Основи тригонометрії
Якщо ви рідко застосовували тригонометрію поза школою, давайте уявно повернемося до часів навчання та ознайомимося з нею знову. Тригонометричні функції дають змогу обчислювати невідомі значення прямокутного трикутника за відомими параметрами. Уявіть, що ви стоїте на землі, дивлячись на високе дерево. Було б дуже важко виміряти висоту дерева із землі. Але якщо ми знаємо кут, під яким ми дивимося вгору на верхівку дерева, і знаємо відстань від себе до дерева, ми можемо вивести висоту самого дерева.

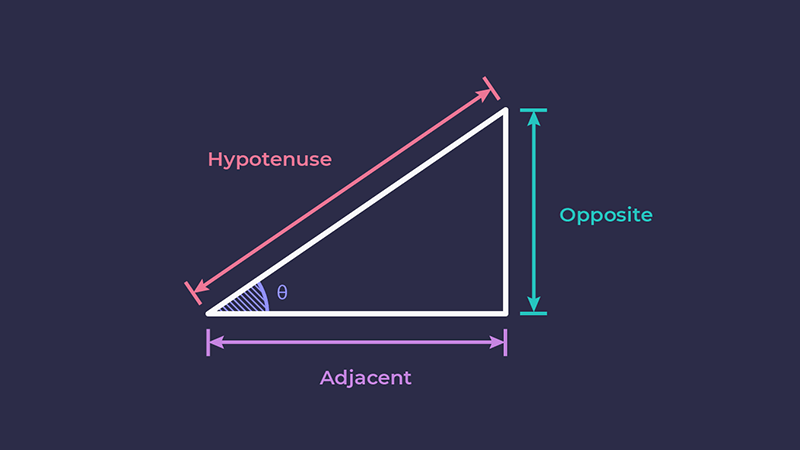
Якщо ми уявляємо цю сцену як трикутник, відома довжина (від нас до дерева) — це прилеглий катет, дерево — це протилежний катет (протилежний куту), а найдовша сторона від нас до вершини дерева називається гіпотенузою.
Синус, косинус і тангенс
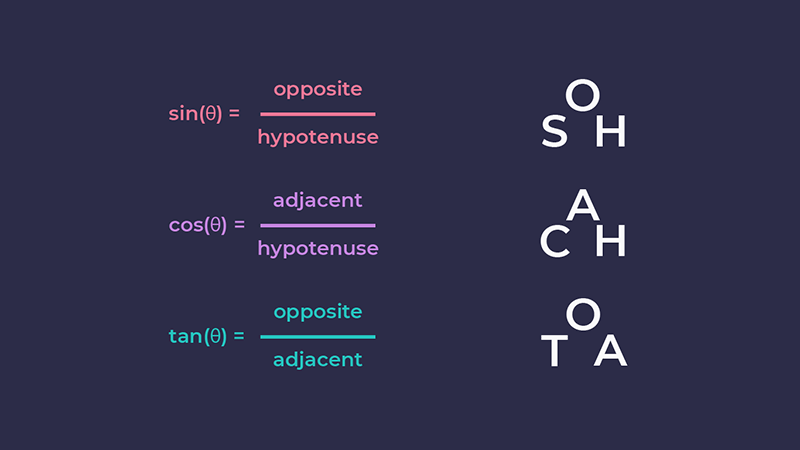
У тригонометрії слід пам'ятати три основні функції: синус, косинус і тангенс (скорочено sin, cos і tan). Вони обчислюються за такими формулами:
sin(angle) = opposite / hypotenuse
cos(angle) = adjacent / hypotenuse
tan(angle) = opposite / adjacent
Кут зазвичай записується грецьким символом тета (θ).
Ми можемо скористатися цими рівняннями, щоб обчислити невідомі значення нашого трикутника з відомих. Щоб виміряти висоту дерева у прикладі, ми знаємо кут (θ) та довжину прилеглого катета.
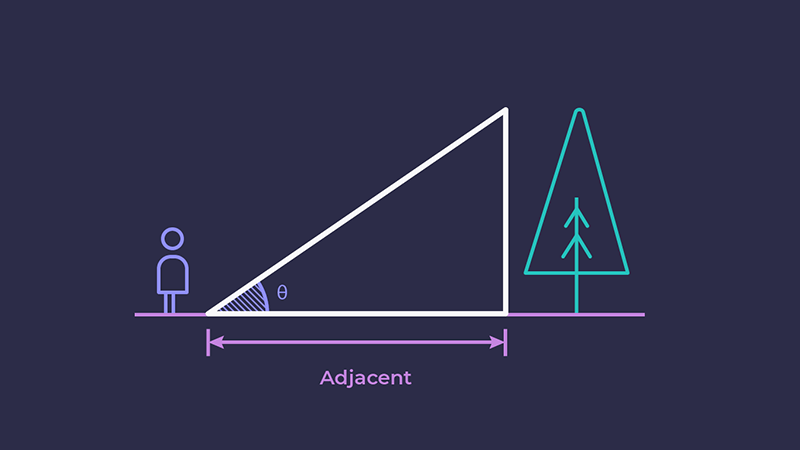
Для обчислення протилежного катета нам знадобиться функція тангенса. Нам потрібно було б поміняти частини формули місцями:
opposite = tan(angle) * adjacent
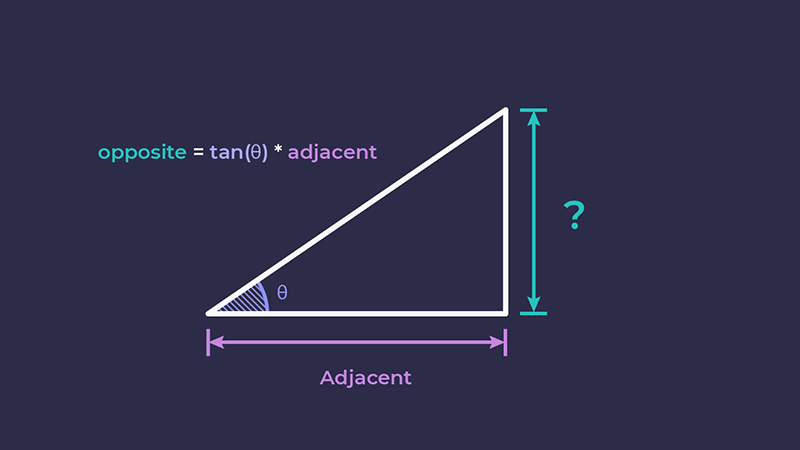
Як отримати tan(θ)? Ми можемо звернутись до інженерного калькулятора (ввести tan, а потім кут) або скористатися кодом! І Sass, і JavaScript включають тригонометричні функції, тож розглянемо деякі способи їх застосування.
Функції SASS
Якщо ми працюємо із заздалегідь визначеними значеннями, то можемо скористатися вбудованими у Sass (препроцесор CSS) тригонометричними функціями.
Щоб включити математичний модуль, нам потрібен такий рядок у нашому SASS:
@use "sass:math";
Ми можемо застосовувати змінні для обчислення протилежного катета за допомогою значень кута та прилеглих катетів.
$angle: 45deg;
$adjacent: 100%;
$opposite: math.tan($angle) * $adjacent;
Функція tan у Sass може використовувати радіани або градуси — якщо використовуються градуси, потрібно вказати одиниці вимірювання, інакше буде застосовано радіани.
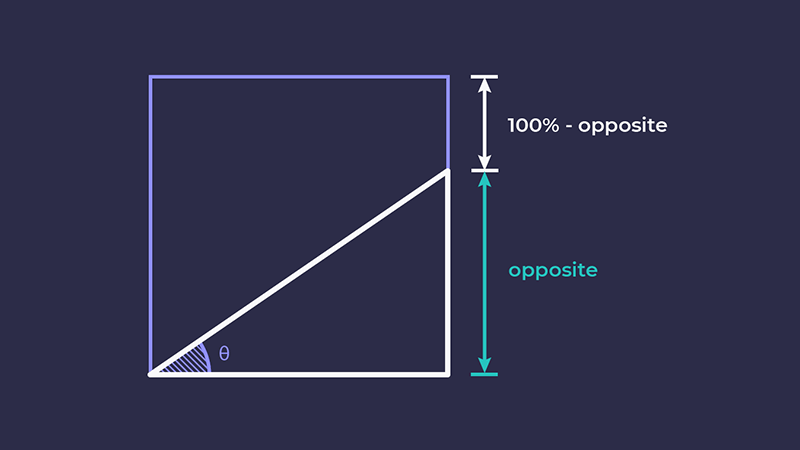
У прикладі далі ми застосовуємо їх у властивості clip-path, щоб визначити координати точок багатокутника (так само як ми обчислювали висоту дерева).
Нам потрібно відняти змінну $opposite від висоти елемента. Так ми отримуємо координату y, оскільки координати clip-path розташовані вздовж осі y і зростають згори до низу.
.element {
clip-path: polygon(0 100%, $adjacent (100% - $opposite), $adjacent 100%);
}
Відсікання рівностороннього трикутника
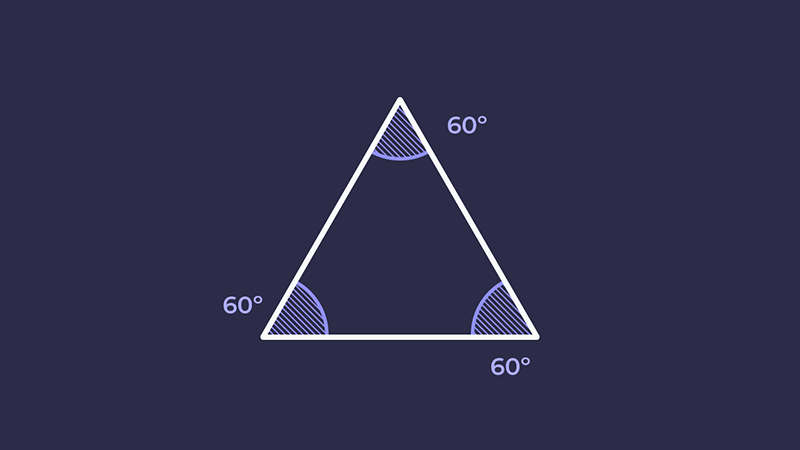
Прямокутний трикутник є найпростішим у тригонометрії. Але ми можемо працювати і з координатами складніших форм, розколюючи їх на прямокутні трикутники. Рівносторонній трикутник — це трикутник з трьома катетами однакової довжини. Можливо, ви пам'ятаєте зі школи, що сума кутів трикутника 180º? Це означає, що кожен кут рівностороннього трикутника дорівнює 60º.
Якщо провести пряму посередині рівностороннього трикутника, ми розділимо його на (як ви вже здогадалися) два прямокутні трикутники. Отже, для трикутника зі сторонами заданої довжини ми знаємо кут (60º), довжину гіпотенузи та довжину прилеглого катета (половину довжини гіпотенузи).

Що нам невідоме — це висота трикутника або ж протилежний катет прямокутного трикутника. Зараз нам потрібно побудувати координати clip-path. Цього разу нам відомі кут і довжина гіпотенузи, тож ми можемо застосувати функцію синус:
$hypotenuse: 60%; // side length
$angle: 60deg;
$opposite: math.sin($angle) * $hypotenuse;
(Ми застосовуємо функцію синус, проте можна скористатися й функцією тангенс, адже ми знаємо, що довжина прилеглого катета — це половина гіпотенузи.) Далі ми можемо застосовувати ці значення для координат clip-path нашого багатокутника:
.element {
clip-path: polygon(
0 $opposite,
($hypotenuse / 2) 0,
$hypotenuse $opposite
);
}
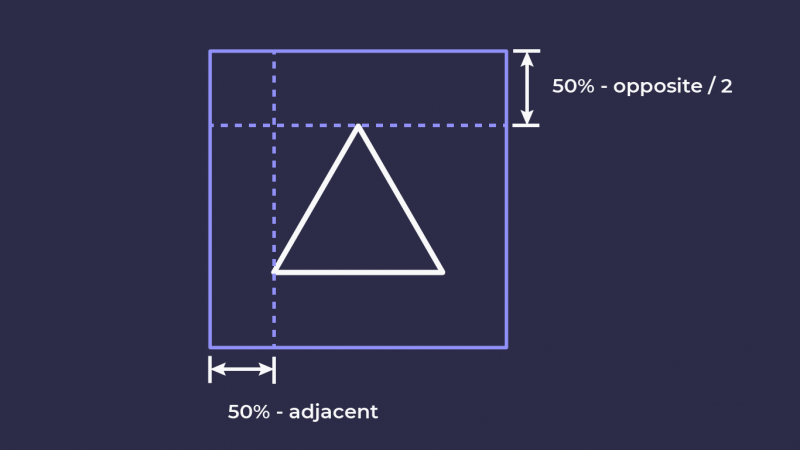
Як ви бачите з прикладу, елемент обрізається з верхнього лівого кута. Це не зовсім те, що нам потрібно: ймовірніше, ми захочемо обрізати його по центру, особливо, якщо це зображення. Ми можемо відповідно налаштувати координати clip-path. Щоб зробити це читабельнішим, ми можемо призначити додаткові змінні для довжини прилеглого катета (половини гіпотенузи), а також початкові та кінцеві координати трикутника:
$hypotenuse: 60%; //side length
$angle: 60deg;
$opposite: math.sin($angle) * $hypotenuse;
$adjacent: $hypotenuse / 2;
$startPosX: (50% - $adjacent);
$startPosY: (50% - $opposite / 2);
$endPosX: (50% + $adjacent);
$endPosY: (50% + $opposite / 2);
.element {
clip-path: polygon(
$startPosX $endPosY,
50% $startPosY,
$endPosX $endPosY
);
}
Створення міксинів для повторного застосування
Це досить складний код до написання для одного трикутника. Створімо міксин Sass, що дасть нам змогу обрізати трикутник будь-якого розміру на будь-який потрібний нам елемент. Оскільки для clip-path досі потрібен префікс у деяких браузерах, наш міксин також міститиме його:
@mixin triangle($sideLength) {
$hypotenuse: $sideLength;
$angle: 60deg;
$opposite: math.sin($angle) * $hypotenuse;
$adjacent: $hypotenuse / 2;
$startPosX: (50% - $adjacent);
$startPosY: (50% - $opposite / 2);
$endPosX: (50% + $adjacent);
$endPosY: (50% + $opposite / 2);
$clip: polygon(
$startPosX $endPosY,
50% $startPosY,
$endPosX $endPosY
);
-webkit-clip-path: $clip;
clip-path: $clip;
}
Щоб відрізати центрований рівносторонній трикутник з будь-якого елемента, ми можемо просто включити міксин, що проходитиме вздовж сторін трикутника:
.triangle {
@include triangle(60%);
}
Обмеження функцій Sass
Застосування функцій SASS має певні обмеження:
- Він передбачає, що змінна
$sideLengthвідома під час компіляції й не допускає динамічних значень. - Sass не дуже добре обробляє одиниці міксинів для наших потреб. В останньому прикладі, якщо ви заміните довжину сторони у відсотках на фіксовану довжину (наприклад, в rem або px), код не працюватиме.
Останнє пов'язано з тим, що наші обчислення для змінних $startPos і $endPos (для центрування clip-path) залежать від віднімання довжини катета від відсотка. На відміну від звичайного CSS (із застосуванням calc()), Sass не дає такої можливості. У останньому прикладі міксин було допасовано так, щоб він працював з будь-якою допустимою одиницею довжини, передавши параметром розмір обрізаного елемента. Потрібно лише впевнитися, що значення для двох переданих параметрів мають однакові одиниці виміру.
Тригонометричні функції CSS
У CSS тригонометричні функції є частиною Модуля значень та одиниць CSS четвертого рівня (наразі в розробці). Вони можуть бути надзвичайно корисними, особливо якщо застосовуються разом зі спеціальними властивостями. Ось як ми могли б переписати наш CSS для застосування вбудованих тригонометричних функцій CSS. Змінити розмір clip path настільки ж просто, як і оновити одну спеціальну властивість:
.triangle {
--hypotenuse: 8rem;
--opposite: calc(sin(60deg) * var(--hypotenuse));
--adjacent: calc(var(--hypotenuse) / 2);
--startPosX: calc(var(--size) / 2 - var(--adjacent));
--startPosY: calc(var(--size) / 2 - var(--opposite) / 2);
--endPosX: calc(var(--size) / 2 + var(--adjacent));
--endPosY: calc(var(--size) / 2 + var(--opposite) / 2);
--clip: polygon(
var(--startPosX) var(--endPosX),
50% var(--startPosY),
var(--endPosX) var(--endPosY)
);
-webkit-clip-path: var(--clip);
clip-path: var(--clip);
}
.triangle:nth-child(2) {
--hypotenuse: 3rem;
}
.triangle:nth-child(2) {
--hypotenuse: 50%;
}
Динамічні змінні
Спеціальні властивості також можуть бути динамічними. Ми можемо змінювати їх за допомогою JS, а залежні від них значення автоматично переобчислюватимуться.
triangle.style.setProperty('--hypotenuse', '5rem')
Тригонометричні функції CSS мають великий потенціал, але, на жаль, вони ще не підтримуються жодним браузером. Щоб зараз користуватися тригонометрію з динамічними змінними, нам потрібен JavaScript.
У наступній статті ми розглянемо деякі з цих можливостей.

Ще немає коментарів