У другій частині цієї серії, присвяченій тригонометрії, ми дослідимо тригонометричні функції JavaScript і дізнаємося, як ми можемо застосовувати їх до нашого коду CSS.
У першій частині ми розглянули основи тригонометрії та дізналися, як можна застосовувати тригонометричні функції у Sass. Але для роботи з динамічними змінними логічніше перемістити наші обчислення до JavaScript. Розгляньмо приклад, який дещо складніший, ніж обрізання простого трикутника.
У цьому прикладі ми маємо квадратну піраміду, побудовану з перетвореннями CSS 3D. За допомогою повзунка ми можемо змінити довжину бічних граней піраміди, через що зміниться загальна висота й кут нахилу бічних граней.
Щоб переобчислити кут, на який обертаються бічні грані, коли змінюється вхідне значення, нам потрібна тригонометрія. Для цього ми можемо взяти бічний переріз піраміди й візуалізувати у вигляді трикутника.

Як і в рівносторонньому трикутнику з попередньої статті, тут можна розбити поперечний переріз нашої піраміди на два прямокутних трикутника. (Цього разу форма поперечного перерізу є рівнобедреним трикутником, тобто має дві сторони однакової довжини.)
Щоб створити фігури для основи та сторін піраміди, ми можемо встановити ширину й початкову висоту та застосувати clip-path для відрізання трикутної форми сторін.
.shape__base {
--w: 10rem;
width: var(--w);
height: var(--w);
}
.shape__side {
width: var(--side);
height: var(--h, 20rem);
clip-path: polygon(50% 0, 100% 100%, 0 100%);
}
Авторка застосовує тут кастомні властивості, тому що вони дозволяють легко повторно застосувати ідентичні значення. Вона встановила --h типовим значенням для властивості height сторони фігури, оскільки це значення пізніше буде замінено за допомогою JavaScript. (Це значення ми отримаємо від повзунка.)
Повертаючись до нашої діаграми перерізу, ми можемо побачити, що відомі нам значення — це протилежний катет (який складатиме половину нашої змінної --w) та гіпотенуза (змінна --h). Невідомим залишається кут, на який нам потрібно повернути сторони, щоб вони сходилися посередині.
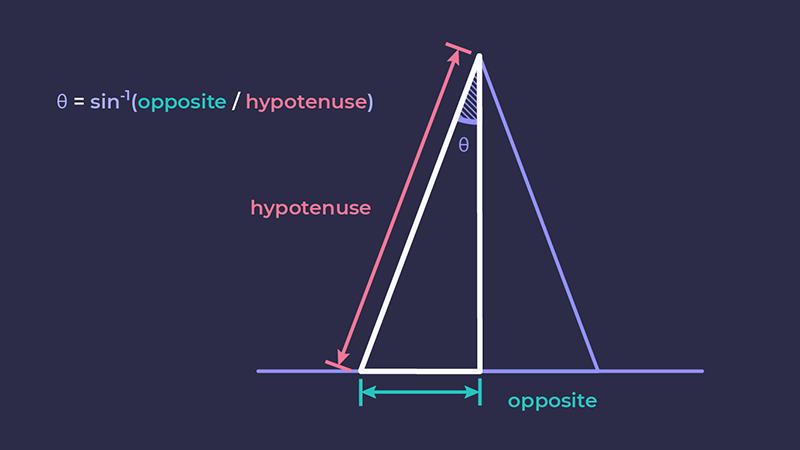
Уявімо, що бічна грань піраміди починається з вихідного положення у центрі. Кут, який нам потрібно обчислити, — це кут вгорі трикутника. Ми можемо порівняти це з прихиленою до стіни драбиною. Кут між драбиною і стіною — це і є той, який нам потрібно обчислити.
Знов таки, ми можемо застосувати кастомні властивості у нашому CSS для встановлення деяких значень перетворення. Кожна сторона матиме однакове значення rotateX() (кут, який ми збираємося обчислити), але різні значення rotateY(), оскільки вони обертатимуться навколо піраміди (тут представлено спеціальну властивість --ry):
.shape__side {
transform-origin: top center;
transform:
rotateY(var(--ry, 0))
rotateX(var(--angle, 15deg));
}
.shape__side:nth-child(2) {
--ry: 90deg;
}
.shape__side:nth-child(3) {
--ry: -90deg;
}
.shape__side:nth-child(4) {
--ry: 180deg;
}
Обчислення кутів
У попередній статті ми бачили, як можна обчислити довжину будь-якої сторони прямокутного трикутника, якщо знаємо кут. А як щодо обчислення самого кута? Для цього нам потрібно переставити наші рівняння.
Нам відома довжина протилежного катета та гіпотенуза, тож ми повинні застосувати функцію синуса. Ділимо протилежний катет на гіпотенузу — і отримуємо sin(ϴ):
sin(angle) = o / h
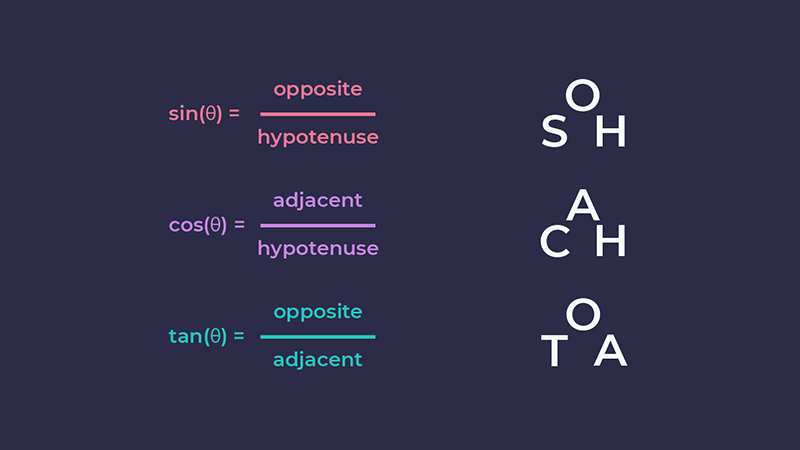
Тому кут обчислюється зворотним синусом (або арксинусом) протилежного катета, поділеного на гіпотенузу:

Математичні функції
Для цього можна скористатись математичними функціями JavaScript. Створімо функцію, яка викликатиметься, коли змінюються вхідні дані та оновлюються кастомні властивості --h (для гіпотенузи) та --angle. Щоб отримати значення Арксинуса, ми скористаємось Math.asin():
const shape = document.querySelector('.shape')
const input = document.querySelector('[data-slider]')
const setAngles = () => {
const o = shape.clientWidth / 2
const h = input.value
const angle = Math.asin(o / h)
shape.style.setProperty('--h', `${h}px`)
shape.style.setProperty('--angle', `${angle}rad`)
}
input.addEventListener('input', setAngles)
Радіани проти градусів
Можливо, ви зауважили, що ми встановили значення власної властивості --angle у радіанах, а не в градусах. Якщо ви не математик, то, найімовірніше, думаєте про кути в градусах, а не в радіанах. Радіан можна візуалізувати як довжину радіуса кола, оберненого по колу. У колі є 2π радіани.
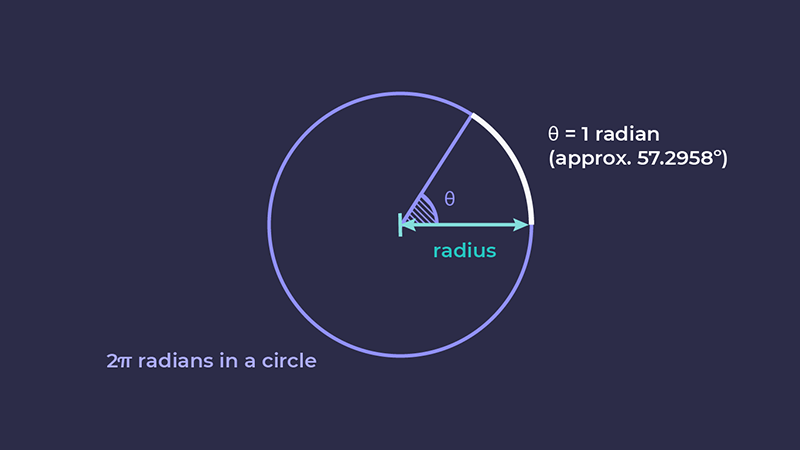
Функція Math.asin() дає нам кут у радіанах, і радіани є цілком нормативними одиницями CSS, тому працюватимуть чудово. Але якщо ви віддаєте перевагу значенням у градусах, ми можемо перетворити їх за допомогою простої функції:
const radToDeg = (radians) => {
return radians * (180 / Math.PI)
}
Також у прикладі отриманий результат округлюється до сотих (двох знаків після коми) за допомогою toFixed():
const setAngles = () => {
const o = shape.clientWidth / 2
const h = input.value
const radians = Math.asin(o / h)
const angle = radToDeg(radians).toFixed(2)
shape.style.setProperty('--h', `${h}px`)
shape.style.setProperty('--angle', `${angle}deg`)
}
Тепер кути сторін нашої піраміди переобчислюватимуться щоразу, коли ми рухаємо повзунком і змінюємо довжину сторін.
Творімо далі
За допомогою цього ж методу ми могли б навіть створити купу пірамід довільної висоти, змінивши одну спеціальну властивість:
Ось ще один приклад творчої тригонометрії в дії: паперова сніжинка, де користувач може перетягувати ручки, щоб закріплювати сегменти трикутника для створення візерунку сніжинки. Координати руху точок було обчислено за допомогою тригонометричних функцій. У наступній статті ми побачимо, як тригонометрія надає нам ще більше творчих можливостей, коли поєднується з JS, і ми можемо створювати багатокутники та складніші форми.

Ще немає коментарів