У статті представлені чотири найпоширеніші алгоритму виявлення контурів.
Перші два, а саме алгоритм трасування квадратів і трасування околиць Мура, прості в реалізації, а тому часто застосовуються для визначення контуру заданого патерну. На жаль, в обох алгоритмів є кілька слабких місць, що призводить до неможливості виявлення контуру великого класу патернів через їх особливий вид суміжності.
 Дані алгоритми будуть ігнорувати всі «дірки» в паттерні. Наприклад, якщо у нас є патерн, подібний показаному на Малюнку 1, виявлений алгоритмами контур буде схожий на показаний на Малюнку 2 (синіми пікселями позначений контур). У деяких областях застосування це цілком допустимо, але в інших областях, наприклад, в розпізнаванні символів, потрібне виявлення внутрішніх частин патерну для знаходження всіх прогалин, які відрізняють конкретний символ. (На Малюнку 3 показаний «повний» контур патерну.)
Дані алгоритми будуть ігнорувати всі «дірки» в паттерні. Наприклад, якщо у нас є патерн, подібний показаному на Малюнку 1, виявлений алгоритмами контур буде схожий на показаний на Малюнку 2 (синіми пікселями позначений контур). У деяких областях застосування це цілком допустимо, але в інших областях, наприклад, в розпізнаванні символів, потрібне виявлення внутрішніх частин патерну для знаходження всіх прогалин, які відрізняють конкретний символ. (На Малюнку 3 показаний «повний» контур патерну.)
Більше про: архітектурні патерни
Отже, для одержання повного контуру спочатку необхідно використовувати алгоритм «пошуку дірок», що визначає отвори в заданому паттерні, а потім застосувати до кожного отвору алгоритм виявлення контурів.

Що таке зв'язність
У цифрових зображеннях з двійковими значеннями піксель може мати одне з наступних значень: 1 — коли є частиною патерну, або 0 — коли є частиною фону, тобто градації сірого відсутні. (Ми будемо вважати, що пікселі зі значенням 1 чорні, а зі значенням 0 — білі).
Для ідентифікації об'єктів на в цифровому паттерні нам потрібно знаходити групи чорних пікселів, «пов'язаних» один з одним. Іншими словами, об'єктами в заданому цифровому паттерні є зв'язкові компоненти цього патерну.
У загальному випадку, зв'язна компонента — це безліч чорних пікселів P, таке, що для кожної пари пікселів pі та pj P існує послідовність пікселів pі, ..., pj, така, що:
a) всі пікселі в послідовності знаходяться в безлічі P, тобто є чорними, і
b) кожні 2 пікселя, що знаходяться в послідовності поруч, є «сусідами».
Виникає важливе питання: коли ми можемо сказати, що 2 пікселя є «сусідами»? Оскільки ми використовуємо квадратні пікселі, відповідь на попереднє питання нетривіальне з наступної причини: квадратної тесселяції пікселі мають спільне або ребро, або вершину, або не мають нічого спільного. У кожного пікселя є 8 пікселів, що мають з ним спільну вершину; такі пікселі складають «околиця Мура» даного пікселя. Чи повинні ми вважати «сусідами» пікселі, що мають тільки одну спільну вершину? Або щоб вважатися «сусідами», два пікселя повинні мати загальне ребро?
Так виникають два види зв'язності, а саме: 4-зв'язність і 8-зв'язність.
4-зв'язність
Коли ми можемо сказати, що заданий безліч чорних пікселів є 4-зв'язковим? По-перше, потрібно визначити поняття 4-сусіда (також званого прямим сусідом):
Визначення 4-сусіда: піксель Q є 4-сусідом заданого пікселя P, якщо Q та P мають спільне ребро. 4-сусіди пікселя P (позначені як P2 P4, P6 та P8), показані на Малюнку 2 нижче.
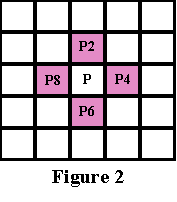
Визначення 4-зв'язної компоненти: безліч чорних пікселів P є 4-зв'язковий компонентою, якщо для кожної пари пікселів pі та pj P існує послідовність пікселів pі, ..., pj, така, що:
a) всі пікселі в послідовності знаходяться в безлічі P, тобто є чорними, і
b) кожні два пікселя, які знаходяться поруч у послідовності є 4-сусідами
Приклади 4-зв'язкових патернів
На малюнку нижче показані приклади 4-зв'язкових патернів:
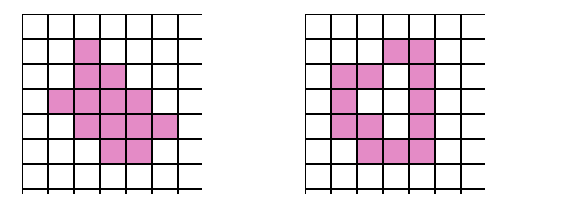
8-зв'язність
Коли можна сказати, що заданий безліч чорних пікселів 8-зв'язне? По-перше, нам потрібно визначити поняття 8-сусіда (також званого непрямим сусідом):
Визначення 8-сусіда: піксель Q є 8-сусідом (або сусідом) заданого пікселя P, якщо Q та P мають спільне ребро або вершину. 8-сусіди заданого пікселя P складають околиця Мура цього пікселя.
Визначення 8-зв'язної компоненти: безліч чорних пікселів P є 8-зв'язковий компонентою (або связной компонентою), якщо для кожної пари пікселів pі та pj P існує послідовність пікселів pі, ..., pj, така, що:
a) всі пікселі в послідовності знаходяться в безлічі P, тобто є чорними, і
b) кожні два пікселя, які знаходяться поруч у цій послідовності є 8-сусідами
Примітка: всі 4-зв'язкові патерни є 8-зв'язковими, тобто 4-зв'язкові патерни є підмножиною безлічі 8-зв'язкових патернів. З іншого боку, 8-цілісний патерн може і не бути 4-зв'язковим.
Приклад 8-зв'язкового патерну
На схемі нижче показаний патерн, який є 8-зв'язковим, але не 4-зв'язковим:
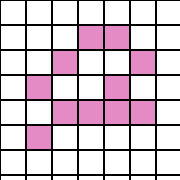
Приклад патерну, не є 8-зв'язковим:
На схемі нижче показаний приклад патерну, який не є 8-зв'язковим, тобто складений з більш ніж однієї зв'язної компоненти (на схемі показані три зв'язкові компоненти):
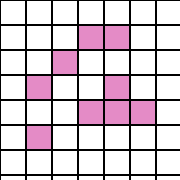
Алгоритм трасування квадратів
Ідея
Що лежить в основі алгоритму трасування квадратів ідея дуже проста; це можна пов'язати з тим фактом, що алгоритм став однією з перших спроб виявлення контуру двійкового патерну.
Щоб зрозуміти, як він працює, потрібно трохи уяви...
Припустимо, у нас є цифровий патерн, наприклад, група чорних пікселів на тлі з білих пікселів, тобто на сітці; знаходимо чорний піксель і оголошуємо його нашим "початковим" пікселем. (Знаходження "початкового" пікселя можна реалізувати безліччю різних способів; ми почнемо з лівого нижнього кута сітки, будемо сканувати кожен стовпець пікселів знизу вгору, від самого лівого стовпця до правого, поки не натрапимо на чорний піксель. Його ми і оголосимо "початковим".)
Тепер уявіть, що ви — божа корівка, що стоїть на початковому пікселі, як це показано на наведеному нижче Малюнку 1. Щоб отримати контур патерну, вам необхідно зробити наступне:
кожен раз, коли ви опиняєтеся на чорному пікселі, повертайте ліворуч, і
кожен раз, коли ви опиняєтеся на білому пікселі, повертайте праворуч,
поки знову не доберетеся до початкового пікселя.
Чорні пікселі, які ви обійшли, будуть контуром патерну.
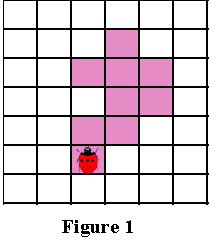
Важливим аспектом алгоритму трасування квадратів є «відчуття напрямку». Повороти вліво і вправо виконуються щодо поточного розташування, яке залежить від того, яким чином ви потрапили на поточний піксель. Отже, щоб робити правильні ходи, необхідно відслідковувати свій напрямок.
Алгоритм
Нижче представлено формальний опис алгоритму трасування квадратів:
Вхідні дані: квадратна тесселяція, T, що містить зв'язну компоненту P чорних клітинок.
Вихідні дані: ряд B (b1, b2 ,..., bk) пікселів кордону, тобто контур.
Початок
- Задаємо B як пусте безліч.
- Скануємо знизу вгору і зліва праворуч клітинки T, поки не буде знайдений чорний піксель s з P.
- Вставляємо s B.
- Робимо поточний піксель p початковим пікселем s.
- Повертаємо вліво, тобто переходимо в сусідній піксель зліва від p.
- Оновлюємо p, тобто він стає поточним пікселем.
- Поки p не дорівнює s, виконуємо
Якщо поточний піксель p є чорним
- вставляємо p B і повертаємо вліво (переходимо в сусідній піксель зліва від p).
- Оновлюємо p, тобто він стає поточним пікселем.
Інакше
- повертаємо вправо (переходимо в сусідній піксель праворуч від p).
- Оновлюємо p, тобто він стає поточним пікселем.
Завершення циклу «Доки»
Кінець
Примітка: поняття «вліво» і «вправо» слід розглядати не відносно сторінки або читача, а щодо напрямку входу в «поточний» піксель під час виконання сканування.
Демонстрація
Нижче показана анімована демонстрація того, як алгоритм трасування квадратів виявляє контур патерну. Не забувайте, що божа корівка рухається по пікселях; помічайте, як змінюється її напрямок при поворотах вліво і вправо. Повороти вліво і вправо виконуються щодо поточного напряму в пікселі, тобто орієнтації божої корівки.

Аналіз
Виявляється, що можливості алгоритму трасування квадратів дуже обмежені. Він здатний виявляти контури великого сімейства патернів, які часто виникають в реальних областях застосування.
В основному це пов'язано з тим, що повороти вліво і вправо не враховують пікселі, розташовані «по
діагоналі» від поточного пікселя.
Давайте розглянемо різні патерни з різною в'язкістю і побачимо, чому терпить невдачу алгоритм трасування квадратів. Крім того, ми вивчимо способи удосконалення можливостей алгоритму і примусимо його працювати хоча б з патернами, що мають особливий вид зв'язності.
Критерій зупинки
Одна з слабкостей алгоритму полягає у виборі критерію зупину. Іншими словами, коли алгоритм припиняє своє виконання?
У вихідному описі алгоритму трасування квадратів умовою завершення є попадання в початковий піксель вдруге. Виявляється, що якщо алгоритм залежить від такого критерію, то він не зможе виявити контури великого сімейства патернів.
Нижче показана анімована демонстрація з поясненням того, як алгоритмом не вдається виявити точний контур патерну з-за поганого вибору критерію зупину:

Як бачите, удосконалення критерію зупинки може стати хорошим початком для поліпшення результативності алгоритму в цілому. Існує дві ефективні альтернативи для наявного критерію зупину:
a) Зупинятися, тільки відвідавши початковий піксель n раз, де n-не менше 2, АБО
b) Зупинятися після потрапляння у початковий піксель вдруге точно так само, як ми потрапили в нього спочатку.
Цей критерій був запропонований Джейкобом Элиософфом, тому ми будемо називати його критерієм зупинки Джейкоба.
Зміна критерію зупинки у загальному випадку покращує результативність алгоритму трасування квадратів, але не дозволяє подолати інші слабкі місця, які він має у разі патернів з особливими видами зв'язності.
Square Tracing Algorithm нездатним виявити контур сімейства патернів зі зв'язністю 8, які НЕ мають зв'язності 4.
Нижче показана анімована демонстрація того, як алгоритму трасування квадратів (з критерієм зупинки Джейкоба) не вдається знайти правильний контур патерну зі зв'язністю 8 без зв'язності 4:

Цей алгоритм абсолютно даремний?
Якщо ви прочитали представлений вище аналіз, то, напевно, думаєте, що алгоритму трасування квадратів не вдається виявити контури більшості патернів. Але виявляється. що існує особливе сімейство патернів, у якого повністю правильно виявляється контур алгоритму трасування квадратів.
Нехай P — безліч чорних пікселів зі зв'язністю 4 на сітці. Нехай білі пікселі сітки, тобто фонові пікселі W теж мають зв'язність 4. Виявляється, що при таких умовах патерну і його фону можна довести, що алгоритм трасування квадратів (з критерієм зупинки Джейкоба) завжди буде успішно справлятися з визначенням контуру.
Нижче представлено доказ, що у випадку, коли і патерн пікселі фону мають пов'язаність 4, алгоритм трасування квадратів буде правильно визначати контур при використанні критерію зупину Джейкоба.
Доказ
Дано: патерн P такий, що всі пікселі патерну (тобто чорні) і пікселі фону (тобто білі) W мають зв'язність 4.
Перше спостереження
Так як безліч білих пікселів W має зв'язність 4, це означає, що в паттерні не може бути ніяких "дірок" (кажучи неформально, "дірками" ми називаємо групи білих пікселів, повністю оточені чорними пікселями патерну).
Наявність будь-якої "дірки" в паттерні призведе до відокремлення групи білих пікселів від інших білих пікселів; при цьому безліч білих пікселів втрачає зв'язність 4.
На Малюнку 2 Малюнку 3 нижче наведено два види "дірок", які можуть виникнути в паттерні зі зв'язністю 4:
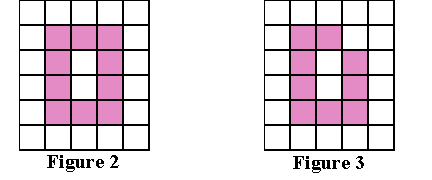
Друге спостереження
Будь-які два чорних пікселя патерну ЗОБОВ'ЯЗАНІ мати одну спільну сторону.
Припустимо, два чорних пікселя мають тільки одну спільну вершину. Тоді, щоб задовольнити властивості 4-зв'язності патерну, повинен існувати шлях, що з'єднує ці два пікселя так, що кожні два сусідніх пікселів на цьому шляху мають зв'язність 4. Але це дасть нам патерн, схожий на Малюнок 3. Іншими словами, це призведе до поділу білих пікселів. Малюнку 4 нижче показаний типовий патерн, що задовольняє припущення, що пікселі патерну і фону 4-пов'язані, тобто не мають "дірок", а кожні два чорних пікселя мають одну спільну сторону:

Корисно представляти такі патерни наступним чином:
Спочатку розглядаємо граничні пікселі, тобто контур патерну. Потім якщо ми розглянемо кожен граничний піксель як має 4 ребра одиничної довжини, то побачимо, що деякі з цих ребер спільні із сусідніми білими пікселями. Ми назвемо такі ребра граничними ребрами.
Такі граничні ребра можна розглядати як ребра багатокутника. Малюнку
5 нижче ця думка продемонстрована на прикладі багатокутника, відповідного паттерну з Малюнка 4 вище:
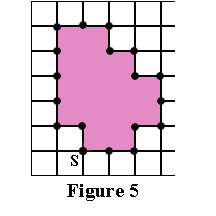
Якщо ми розглянемо всі можливі конфігурації» граничних пікселів, які можуть виникати в таких паттернах, то побачимо, що існує два простих випадку, показаних на Рисунку 6 та Малюнку 7 нижче.
Граничні пікселі можуть бути кратними цих випадків або іншими розташуванням, тобто поворотами цих двох випадків. Граничні ребра помічені синім E1, E2, E3 та E4.
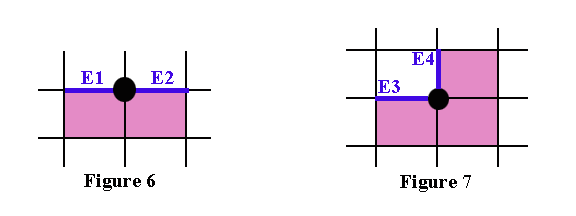
Третє спостереження
У разі розглянутих вище двох випадків, якою б початковий піксель ми не вибрали, і в якому б напрямку в нього не потрапили, алгоритм трасування квадратів ніколи не буде «повертатися назад» (backtrack), ніколи не буде «проходити через» граничне ребро двічі (якщо він не трасує кордон вдруге) і ніколи не пропустить граничне ребро. Перевірте!
Тут потрібно пояснити дві концепції:
a) алгоритм «повертається назад», коли перед трасуванням всій кордону він йде назад, щоб відвідати вже відвіданий піксель, і
b) для кожного граничного ребра існує два способи «пройти через нього», а саме «всередину» і «назовні» (де «всередину» позначає рух всередину відповідного багатокутника, а «назовні» — назовні багатокутника).
Крім того, коли алгоритм проходить «всередину» через одне з граничних ребер, він пройде «назовні» через таке граничне ребро, тобто алгоритм трасування квадратів не повинен мати можливості пройти крізь два послідовних ребра однаковим чином.
Останнє спостереження
У кожного патерну існує парна кількість граничних ребер.
Якщо подивитися на многокутник з Малюнка 5, то можна побачити, що:
якщо ми хочемо почати з вершини S, зазначеної на схемі, і слідувати за граничним ребрах, поки знову не досягнемо S, то зауважимо, що перетнемо в процесі парна кількість граничних ребер. Можна вважати кожне граничне ребро «кроком» в окремому напрямку. Тоді для кожного «кроку» вправо повинен бути відповідний «крок вліво, якщо ми хочемо повернутися у вихідну позицію. Те ж саме відноситься до вертикальних «кроків». Отже, «кроки» повинні мати відповідні пари і це пояснює, чому у кожному з таких патернів буде парна кількість граничних ребер.
Отже, коли алгоритм трасування квадратів входить через початкова граничне ребро (початкового пікселя) вдруге, то він буде це робити в тому напрямі, що і в перший раз.
Причина цього в тому, що оскільки існує два способи проходу через граничне ребро, і алгоритм поперемінно виконує рух «всередину» і «назовні», а граничних ребер парна кількість, то алгоритм пройде через початкове граничне ребро вдруге так само, як і в перший.
Висновок
У випадку 4-зв'язкового патерну і фону алгоритм трасування квадратів виявить всю кордон, тобто контур, патерну і припинить роботу після одноразової трасування, тобто не буде трасувати її заново, оскільки при досягненні початкового граничного ребра вдруге він увійде в нього так само, як і в перший раз. Отже, алгоритм трасування квадратів з критерієм зупинки Джейкоба буде правильно визначати контру будь-якого патерну за умови, що і патерн, і фон мають 4-зв'язністю.
Трасування околиць Мура
Ідея
Ідея, що лежить в основі трасування околиць Мура (Moore-Neighbor tracing), проста; але перш ніж пояснювати її, нам потрібно пояснити важливе поняття: околиці Мура пікселя.
Околиця Мура
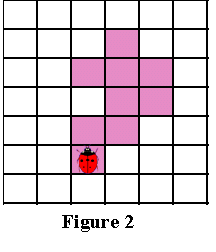
Околиця Мура пікселя P — це безліч з 8 пікселів, що мають спільну вершину або ребро з цим пікселем. Такі пікселі, а саме P1, P2, P3, P4, P5, P6, P7 і P8, показані на Малюнку 1.
Околиця Мура (Moore neighborhood, також звана 8-сусідами або indirect сусідів (непрямими сусідами)) — це важливе поняття, що часто згадується в літературі.

Тепер ми готові познайомитися з ідеєю, що лежить в основі трасування околиць Мура.
Нехай існує цифровий патерн, тобто група чорних пікселів, на тлі з білих пікселів, тобто на сітці; знайдемо чорний піксель і оголосимо його "початковим" пікселем. (Знаходити "початковий" піксель можна різними способами, але ми, як і раніше, будемо починати з лівого нижнього кута і сканувати всі стовпці пікселей по черзі, поки не знайдемо перший чорний піксель, який і оголосимо "початковим".)
Читайте також про Жадібні алгоритми
Тепер знову уявіть, що ви божа корівка, що стоїть на початковому пікселі, як показано на Малюнку 2 нижче. Без втрати узагальненості ми будемо виявляти контур, рухаючись навколо патерну за годинниковою стрілкою. (Неважливо, який напрямок ми оберемо, головне — використовувати його в алгоритмі постійно).
Загальна ідея полягає в наступному: кожен раз, коли ми потрапляємо в чорний піксель P, то повертаємося назад, тобто до білого пікселю, в якому стояли раніше. Потім обходимо піксель P за годинниковою стрілкою, відвідуючи кожен піксель в його околиці Мура, поки не потрапимо в чорний піксель. Алгоритм завершує виконання, коли початковий піксель досягає початкового пікселя вдруге.
Ті чорні пікселі, які відвідав алгоритм, будуть контуром патерну.
Алгоритм
Нижче наведено формальний опис алгоритму трасування околиць Мура:
Вхідні дані: квадратна тесселяція T, що містить зв'язну компоненту P з чорних клітинок.
Вихідні дані: ряд B (b1, b2 ,..., bk) граничних пікселів, тобто контур.
Позначимо як M(a) околиця Мура пікселя a.
Нехай p буде поточним граничним пікселем.
Нехай c буде поточним розглядаються пікселем, тобто c знаходиться у M(p).
Початок
- Задаємо B як пусте безліч.
- Знизу вгору і зліва направо скануємо клітинки T, поки не знайдемо чорний піксель s з P.
- Вставимо s B.
- Задамо в якості поточної граничної точки p крапку s, тобто p=s
- Повернемося назад, тобто перейдемо до пікселя, з якого ми прийшли в s.
- Задамо як c наступний за годинниковою стрілкою піксель M(p).
- Поки c не дорівнює s, виконуємо
- якщо c — чорний
- Вставляємо c B
- задаємо p=c
- повертаємося назад (переміщуємо поточний піксель c піксель, з якого потрапили у p)
Інакше
- переміщуємо поточний піксель c наступного за годинниковою стрілкою піксель M(p)
Кінець циклу «Доки»
Кінець
Демонстрація
Нижче показана анімована демонстрація того, як трасування околиць Мура виконує виявлення контуру патерну. (Ми вирішили трасувати контур за годинниковою стрілкою.)

Аналіз
Основна слабкість трасування околиць Мура полягає у виборі критерію зупину.
У вихідному описі алгоритму для трасування околиць Мура критерієм зупинки є попадання в початковий піксель вдруге. Аналогічно алгоритму трасування квадратів, виявляється, що трасування околиць Мура при використанні такого критерію не може виявляти контури великого сімейства патернів.
Нижче показана анімована демонстрація, яка пояснює, чому алгоритмом не вдається знайти точний контур патерну з-за поганого вибору критерію зупину:

Як бачите, удосконалення критерію зупинки може стати хорошим початком для поліпшення результативності трасування в цілому. Для критерію зупину є дві ефективні альтернативи, аналогічні критерію зупину Джейкоба.
Використання критерію Джейкоба значно покращує результативність трасування околиць Мура, роблячи його найкращим алгоритмом для визначення контуру будь-якого патерну, незалежно від його зв'язності.
Причина цього в основному полягає в тому, що для пошуку наступного граничного пікселя алгоритм перевіряє всю околицю Мура граничного пікселя. На відміну від алгоритму трасування квадратів, який робить повороти тільки вліво і вправо і втрачає пікселі «по діагоналі», трасування околиць Мура завжди буде здатна виявити зовнішню кордон будь зв'язної компоненти. Причина полягає в наступному: для будь-якого 8-зв'язкового (або зв'язкового) патерну наступний граничний піксель лежить в межах околиці Мура поточного граничного пікселя. Оскільки трасування околиць Мура перевіряє кожен піксель в околиці Мура поточного граничного пікселя, вона зобов'язана виявити наступний граничний піксель.
Коли трасування околиць Мура досягає початкового пікселя вдруге точно так само, як вона зробила це в перший раз, то це значить, що був виявлений повний зовнішній контур патерну, і якщо не зупинити алгоритм, то він заново буде виявляти той же контур.
Радіальна розгортка
Алгоритм радіальної розгортки (Radial Sweep) — це алгоритм виявлення контуру, розглянутий в деяких книгах. Незважаючи на складну назву, що лежить в його основі ідея дуже проста. Насправді, виявляється, що алгоритм радіальної розгортки ідентичний трасуванні околиць Мура. Можна задатися питанням: «Навіщо ж взагалі ми його згадуємо?».
Трасування околиць Мура виконує пошук в околиці Мура поточного граничного пікселя в певному напрямку (ми вибрали напрямок за годинниковою стрілкою), поки не знайде чорний піксель. Потім вона оголошує цей піксель поточним граничним пікселем і продовжує роботу.
Алгоритм радіальної розгортки виконує те ж саме. З іншого боку, він забезпечує цікавий спосіб пошуку наступного чорного пікселя в околиці Мура заданого граничного пікселя.
Спосіб заснований на наступній ідеї:
кожен раз, коли ми знаходимо новий граничний піксель, робимо його поточним пікселем P і малюємо уявний відрізок прямої, що з'єднує P з попереднім граничним пікселем. Потім повертаємо відрізок щодо P за годинниковою стрілкою, поки він не натрапить на чорний піксель в околиці Мура пікселя P. Поворот відрізка ідентичний перевірці кожного пікселя в околиці Мура P.
Ми створили анімовану демонстрацію того, як працює алгоритм радіальної розгортки і чим він схожий на трасування околиць Мура.

А коли зупиняється алгоритм радіальної розгортки?
Давайте пояснимо поведінка алгоритму при використанні наступних критеріїв зупинки...
Критерій зупинки 1
Нехай алгоритм радіальної розгортки завершує роботу тоді, коли відвідає початковий піксель вдруге.
Нижче представлена анімована демонстрація, з якої зрозуміло, чому правильно буде змінити критерій зупинки.

Варто згадати також те, що при використанні цього критерію зупину в обох алгоритмах результативність алгоритму радіальної розгортки ідентична трасуванні околиць Мура.
В алгоритмі трасування квадратів і трасуванні околиць Мура ми з'ясували, що використання критерію зупину Джейкоба значно покращує результативність обох алгоритмів.
Критерій зупинки Джейкоба вимагає, щоб алгоритм припиняв виконання при відвідуванні початкового пікселя вдруге в тому ж напрямку, що і в перший раз.
На жаль, ми не можемо використовувати в алгоритмі радіальної розгортки критерій зупинки Джейкоба. Причина полягає в тому, що алгоритм радіальної розгортки не визначає поняття «напряму», в якому він потрапляє в граничний піксель. Іншими словами, незрозуміло «напрям», в якому алгоритм потрапив в граничний піксель (і його визначення нетривіально).
Отже, нам потрібно запропонувати інший критерій зупинки, який не залежить від напрямку попадання в певний піксель, здатний поліпшити результативність алгоритму радіальної розгортки...
Критерій зупинки 2
Припустимо, що кожен раз, коли алгоритм виявляє новий граничний піксель Pі, він вставляється у низку граничних пікселів: P1, P2, P3, ..., Pі; і оголошується поточним граничним пікселем. (P1 ми будемо вважати початковим пікселем). Це означає, що ми знаємо попередній граничний піксель Pi-1 кожного поточного граничного пікселя Pі . (Що стосується початкового пікселя, то ми будемо припускати, що P0 є уявним пікселем, нееквівалентним жодному з пікселів на сітці, який стоїть перед початковим пікселем у ряду граничних пікселів).
З урахуванням представлених вище припущень ми можемо визначити критерій зупинки наступним чином:
Алгоритм припиняє виконання, коли:
a) поточний граничний піксель Pі вже раніше зустрічався як піксель Pj (де j < i ) в ряду граничних пікселів, І
b) Pi-1 = Pj-1.
Іншими словами, алгоритм завершує виконання тоді, коли він відвідує граничний піксель P у другий раз, якщо граничний піксель P (в ряду граничних пікселів) вдруге є тим же пікселем, який був до P, коли P був відвіданий у перший разів.
Якщо умова критерію зупину задоволено і алгоритм не завершує роботу, то алгоритм радіальної розгортки буде продовжувати виявляти ту ж кордон вдруге.
Результативність алгоритму радіальної розгортки з цим критерієм зупинки схоже з результативністю трасування околиць Мура з критерієм зупинки Джейкоба.
Алгоритм Тео Павлідіса
Ідея
Цей алгоритм — один із самих останніх алгоритмів виявлення контурів, запропонований Тео Павлідісом. Він привів його у своїй книзі 1982 року Algorithms for Graphics and Image Processing (глава 7, розділ 5). Він не такий простий, як алгоритм трасування квадратів або трасування околиць Мура, але не так вже і складний (це властиво більшості алгоритмів виявлення контурів).
Цей алгоритм ми будемо пояснювати не так, як це зроблено в його книзі. Наш підхід легше сприймається і він дає уявлення про загальну ідею, що лежить в основі алгоритму.
Без втрати узагальненості ми вирішили обходити контур за годинниковою стрілкою, щоб відповідати порядку всіх інших алгоритмів, представлених у статті. З іншого боку, Павлідіс вибрав напрямок проти годинникової стрілки. На результативність алгоритму це ніяк не вплине. Єдина відмінність полягає у відносному напрямку рухів, які ми будемо робити при обході контуру.
Тепер перейдемо до ідеї...
Припустимо, у нас є цифровий патерн, тобто група чорних пікселів на тлі з білих пікселів, тобто на сітці; знаходимо чорний піксель і оголошуємо його "початковим" пікселем. Шукати "початковий" піксель можна різними способами, наприклад, викладеним вище.
Для знаходження початкового пікселя користуватися цим способом необов'язково. Замість цього ми виберемо початковий піксель, що задовольняє наступним обмеженням, що накладається на вибір початкового пікселя алгоритмом Павлідіса:
Важливе обмеження напрямку, в якому ми входимо в початковий піксель
Насправді можна вибрати БУДЬ-чорний граничний піксель як початкового при такій умові: коли ви спочатку стоїте на ньому, лівий сусідній піксель НЕ чорний. Іншими словами, потрібно входити в початковий піксель в такому напрямку, щоб лівий сусідній піксель був білим («лівий» тут береться щодо напрямку, в якому ми входимо в початковий піксель).
Тепер уявімо, що ви божа корівка, що стоїть на початковому пікселі, як це показано на Малюнку 1 нижче. В процесі виконання алгоритму нас будуть цікавити тільки три пікселя, що знаходяться перед вами, тобто P1, P2 та P3, показані на Малюнку 1. (Ми позначимо як P2 піксель перед вами, P1 — це піксел ліворуч від P2, а P3 — піксель праворуч від P2).
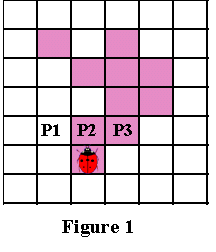
Як і в алгоритмі трасування квадратів, найважливіше в алгоритмі Павлідіса — це «відчуття напрямку». Повороти вліво і вправо виконуються щодо поточної позиції, яка залежить від того, як ви увійшли в поточний піксель. Отже, щоб робити правильні ходи, важливо відслідковувати поточну орієнтацію. Але як би ви не були розташовані, пікселі P1, P2 і P3 визначаються описаним вище чином.
Маючи цю інформацію, ми готові до пояснення алгоритму...
Кожен раз, коли ви стоїте на поточному граничному пікселі (який спочатку є початковим пікселем), робимо наступне:
По-перше, перевіряємо піксель P1. Якщо P1 чорний, тоді оголошуємо P1 поточним граничним пікселем і переміщаємося на один крок вперед, а потім робимо крок вліво, щоб опинитися на P1 (порядок ходів дуже важливий).
Малюнку 2 нижче показаний цей випадок. Шлях, по якому потрібно потрапити у P1, показаний синім.
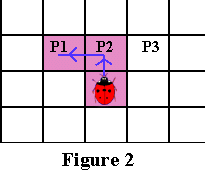
І тільки якщо P1 білий, переходимо до перевірки P2...
Якщо P2 чорний, то оголошуємо P2 поточним граничним пікселем і рухаємося на крок вперед, щоб опинитися на P2. Цей випадок показаний на Малюнку 3 нижче. Шлях, яким треба рухатися на P2, показаний синім.
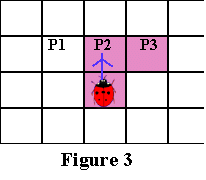
Тільки якщо і P1 і P2 білі, переходимо до перевірки P3...
Якщо P3 чорний, то оголошуємо P3 поточним граничним пікселем і рухаємося на один крок вправо, а потім на один крок вліво, як показано на Малюнку 4.
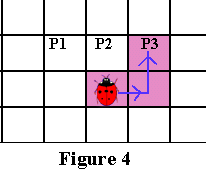
Ось і все! Три простих правила для трьох простих випадків. Як бачите, важливо відслідковувати свій напрямок при поворотах, тому що всі ходи робляться щодо поточної орієнтації. Але, здається, ми щось забули? Що якщо всі три пікселя перед нами білі? Тоді ми повертаємося (стоячи на поточному граничному пікселі) на 90 градусів за годинниковою стрілкою, щоб побачити перед собою новий набір з трьох пікселів. Потім ми виконуємо ту ж перевірку для цих нових пікселів. У вас може все одно залишитися питання: що якщо всі ці три пікселя будуть білими?! Тоді знову повертаємося на 90 градусів за годинниковою стрілкою, стоячи на тому ж пікселі. Перш ніж перевірити всю околицю Мура пікселя, можна повернутися три рази (щоразу на 90 градусів за годинниковою стрілкою).
Якщо ми обернемося три рази, так і не знайшовши чорних пікселів, то це означає, що ми стоїмо на ізольованому пікселі, не сполученому ні з яким іншим чорним пікселем. Саме тому алгоритм дозволяє повернутися три рази, а потім завершує своє виконання.
Ще один аспект: Коли алгоритм завершує виконання?
Алгоритм завершує роботу в двох випадках:
a) як сказано вище. алгоритм дозволяє повернутися три рази (щоразу на 90 градусів за годинниковою стрілкою), після його завершує виконання і оголошує піксель ізольованим, АБО
b) коли поточний граничний піксель є початковим пікселем, алгоритм завершує виконання, «оголошуючи», що виявив контур патерну.
Алгоритм
Нижче представлено формальний опис алгоритму Павлідіса:
Вхідні дані: квадратна тесселяція T, що містить зв'язну компоненту P чорних клітинок.
Вихідні дані: ряд B (b1, b2 ,..., bk) граничних пікселів, тобто контур.
Визначення:
- Позначимо як p поточний граничний піксель, тобто піксель, на якому ми стоїмо.
- Визначимо P1, P2 та P3 наступним чином: (див. Малюнок 1 вище)
- P2 — це піксель перед вами, сусідній з тим, на якому ви стоїте, тобто з пікселем p.
- P1 — лівий піксель, сусідній з P2.
- P3 — правий піксель, сусідній з P2.
- Визначимо «крок» в заданому напрямку переміщення на відстань одного пікселя в цьому напрямку.
Початок
- Задаємо B як пусте безліч.
- Скануємо клітинки T знизу вгору і зліва направо, поки не буде знайдений чорний початковий піксель s з P (див. вище важливе обмеження щодо напрямку, в якому ми потрапляємо в початковий піксель)
- Вставляємо s B.
- Задаємо поточний піксель p в якості початкового пікселя s.
- Повторюємо наступне:
Якщо піксель P1 чорний
- Вставляємо P1 B
- Оновлюємо p=P1
- Рухаємося на один крок вперед, а потім робимо крок вліво
інакше якщо P2 чорний
- Вставляємо P2 B
- Оновлюємо p=P2
- Переміщаємося на один крок вперед (див. вище Малюнок 3)
інакше якщо P3 чорний
- Вставляємо P3 B
- Оновлюємо p=P3
- Робимо один крок вправо, оновлюємо позицію і переміщаємося вліво (див. вище Малюнок 4)
інакше, якщо ми вже тричі повернулися на 90 градусів за годинниковою стрілкою, перебуваючи у одному пікселі p
- завершуємо виконання програми і оголошуємо p ізольованим пікселем
інакше
- повертаємося на 90 градусів за годинниковою стрілкою, стоячи на поточному пікселі p
Поки p=s (Завершуємо цикл повтору)
Кінець
Демонстрація
Нижче показана анімована демонстрація того, як алгоритм Павлідіса виявляє контур заданого патерну. Не забувайте, що ми ходимо по пікселях; помічайте, як змінюється орієнтація при поворотах ліворуч або праворуч. Щоб пояснити алгоритм як можна докладніше, ми включили в нього всі можливі випадки.

Аналіз
Якщо ви вважаєте, що алгоритм Павлідіса ідеальний для виявлення контурів патернів, то вам варто змінити свою думку...
Цей алгоритм дійсно трохи складніше, ніж, припустимо трасування околиць Мура, в якій немає особливих випадків, що вимагають окремої обробки, проте йому не вдасться визначити контури великого сімейства патернів, що має певний вид зв'язності.
Алгоритм дуже добре працює на 4-зв'язкових паттернах. Його проблема виникає при трасуванні деяких 8-зв'язкових патернів, які не є 4-зв'язковими. Нижче показана анімована демонстрація того, як алгоритмом Павлідіса не вдається знайти правильний контур 8-зв'язкового патерну (не є 4-зв'язковим) — він пропускає більшу частину кордону.

Існує два простих способи зміни алгоритму для значного поліпшення його результативності.
a) Замінити критерій зупинки
Замість того, щоб завершувати алгоритм, коли він відвідує початковий піксель вдруге, можна завершувати його, коли він відвідає початковий піксель в третій або навіть четвертий раз. Це поліпшить загальну результативність алгоритму.
АБО
b) Дістатися до джерела проблеми, а саме, до вибору початкового пікселя
Існує важливе обмеження щодо напрямку, в якому виконується вхід в початковий піксель. По суті, потрібно увійти в початковий піксель так, щоб коли ти стоїш на ньому, піксел ліворуч від тебе є білим. Причина введення цього обмеження така: оскільки ми завжди розглядаємо три пікселя перед нами у певному порядку, в деяких паттернах ми будемо пропускати граничний піксель, що лежить безпосередньо зліва від початкового пікселя.
Ми ризикуємо пропустити не тільки лівий сусідній піксель від початкового пікселя, але і піксель безпосередньо під ним (як продемонстровано в аналізі). Крім того, в деяких паттернах буде пропущено піксель, відповідний пікселю R Малюнку 5 нижче. Отже, ми припускаємо, що в початковий піксель потрібно потрапляти в такому напрямку, щоб пікселі, відповідні пікселям L, W та R, показаним на Малюнку 5 нижче, були білими.

В такому випадку патерни зразок показаного в демонстрації будуть виявлятися правильно і результативність алгоритму Павлідіса значно покращиться. З іншого боку, пошук початкового пікселя, що задовольняє таким вимогам, може бути складним завданням, і в багатьох випадках такого пікселя знайти буде неможливо. В цьому випадку слід використовувати альтернативний спосіб поліпшення алгоритму Павлідіса, а саме завершення алгоритму після відвідування початкової точки в третій раз.


Ще немає коментарів