Сьогодні розглянемо модель навчання без нагляду, відому як самоорганізована карта, або Self-Organizing Maps (SOM), а також її реалізацію на Python. Ми будемо використовувати приклад кольорової моделі RGB для навчання SOM і демонстрації її швидкодії та типового використання.
Загальні поняття
Самоорганізовану карту вперше представив Теуво Кохонен у 1982 році. Також вона іноді називається картою Кохонена. Це особливий тип штучної нейронної мережі, який створює карту навчальних даних. Карта, як правило, це двовимірна прямокутна сітка вузлів різної ваги, але вона може бути розширена до тривимірної або вищої розмірної моделі. Можливі й інші структури сітки, наприклад, гексагональна.
SOM переважно застосовується для візуалізації даних та наочно показує зібрані навчальні зразки. У двовимірній прямокутній сітці кожна клітина представлена вагою вектора. Для тренувальних SOM кожна вага клітини — це підсумок кількох прикладів навчання. Суміжні клітини мають аналогічні ваги, а приклади можуть бути асоційовані з клітинками, які розташовані поруч.
На малюнку схематично зображено структуру SOM:
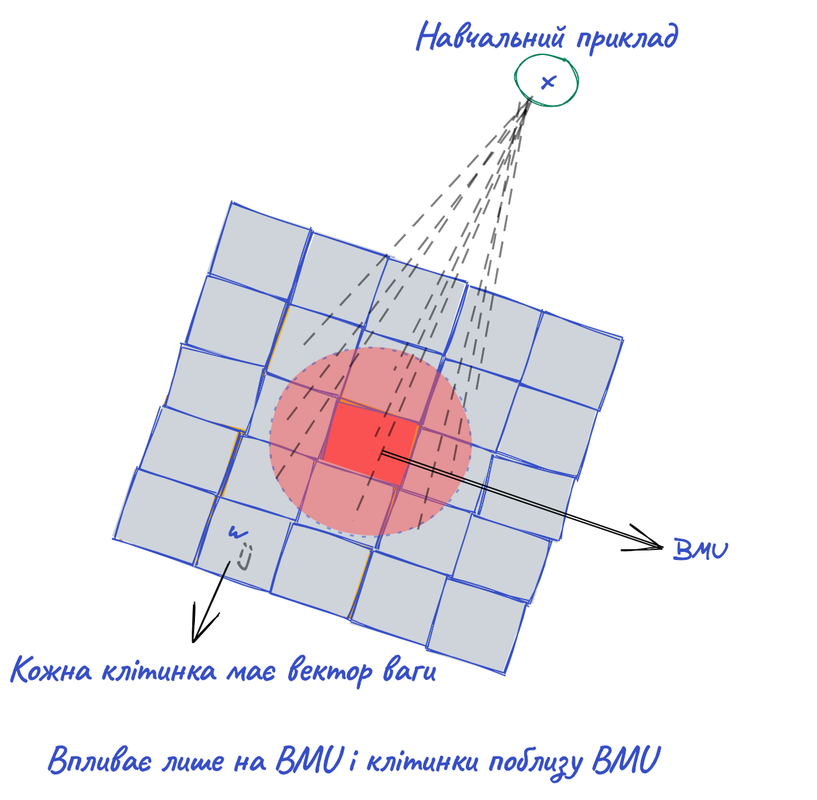
SOM тренується за допомогою конкурентного навчання.
Конкурентне навчання — це форма навчання без нагляду, коли складові елементи змагаються за задовільний результат і лише один може перемогти.
Коли навчальний приклад вводиться в сітку, визначається найвідповідніший вузол (BMU) (переможець змагання). BMU — це клітинка, чия вага ближче до навчального прикладу.
Далі, ваги BMU та ваги сусідніх з ними клітинок адаптовуються, щоб стати ближче до введеного навчального екземпляра. Хоча є й інші робочі варіанти навчання, тут ми представляємо найпопулярнішу реалізацію SOM.
Нам знадобляться деякі підпрограми Python для демонстрації функцій, що використовуються для навчання SOM. Тож імпортуймо кілька потрібних нам бібліотек:
import numpy as np
import matplotlib.pyplot as plt
Алгоритм навчання самоорганізованими картами
Базовий алгоритм навчання SOM:
- Ініціалізуються всі ваги сітки SOM.
- Повтор до досягнення конвергенції (збіжності) або максимальної кількості періодів:
- Перемішуються приклади навчання.
- Для кожного навчального екземпляра x:
- Пошук найвідповіднішої одиниці BMU.
- Оновлення ваги вектора BMU та сусідніх з ним клітинок.
Три кроки для ініціалізації, пошук BMU та оновлення ваги описано в наступних розділах, тож почнімо!
Ініціалізація СІТКИ SOM
Всі ваги сітки SOM можна ініціалізувати у випадковому порядку. Ваги сітки SOM також можна ініціалізувати у випадковий спосіб вибраними прикладами з тренувального набору даних.
Які варто обрати?
SOM чутливі до початкової ваги карти, тому цей вибір впливає на всю модель. Відповідно до дослідження університету Лестер та Сибірського федерального університету:
Порівнюючи частку кінцевої карти SOM RI (випадкова ініціалізація), яка перевершила PCI (ініціалізація основних компонентів) за тих самих умов, було помічено, що RI працює досить добре для нелінійних наборів даних. Однак для квазілінійних наборів даних результат залишається непереконливим. Загалом, можна зробити висновок, що гіпотеза про переваги PCI хибна для нелінійних наборів даних.
Для нелінійних наборів даних випадкова ініціалізація краща за невипадкову. Для квазілінійних наборів даних жоден з підходів не має явних переваг. З огляду на це ми обираємо випадкову ініціалізацію.
Пошук найвідповіднішого вузла (BMU)
Найкраща відповідна одиниця — це клітина сітки SOM, яка розташована найближче до навчального прикладу x. Один з методів пошуку цієї одиниці — обчислення евклідової відстані x від ваги кожної клітини сітки.
Клітинку з найменшою віддаллю можна вибрати як BMU.
Важливо зазначити, що евклідова відстань — це не єдиний метод вибору BMU. Альтернативна міра віддалі або показник подібності також можуть бути корисними для визначення BMU. Цей вибір в основному залежить від даних та моделі, яку ви створюєте.
Оновлення вектора ваги BMU та сусідніх клітинок
Навчальний приклад x зачіпає різні клітинки сітки SOM, він притягує ваги цих клітинок до себе. Максимальна зміна відбувається в BMU, а вплив x зменшується, коли ми віддаляємося від BMU у сітці SOM. Для клітини з координатами (i, j), його вага wij оновлюється у період t + 1 як:
[ w_{ij}^{(t+1)} ← w_{ij}^{(t)} + Δw_{ij}^{(t)} ]
Де (Δw_{ij}^{(t)} ) – це зміна, яка буде додана до ( w_{ij}^{(t)} ). Її можна обчислити так:
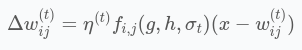
У цьому виразі:
- t – номер періоду;
- (g, h) – координати BMU;
- η – швидкість навчання;
- ( σ_{t} ) – радіус;
- (f_{ij}(g,h,σ_{t}) )– функція відстані до сусідів.
У наступних розділах ми докладніше розберемо цей вираз тренування з вагою.
Швидкість навчання
Швидкість навчання η — це константа в діапазоні [0,1], вона визначає розмір кроку ваги вектора відносно введеного тренувального прикладу. Для η = 0 немає ніяких змін у вазі, а коли η = 1, вага вектора ( w_{ij} ) бере значення x.
η залишається на високому рівні спочатку, а тоді згасає в міру розвитку періодів. Однією зі стратегій зниження швидкості навчання на етапі навчання — використання експоненціального спаду:
[ η^{(t)} = η^{0}e^{(−ttimes λ)} ]
Де λ < 0 — швидкість спадання.
Щоб зрозуміти, як змінюється швидкість навчання за допомогою темпу спадання, сплануймо швидкість навчання у різних періодах, коли початкова швидкість — це одиниця:
epochs = np.arange(0, 50)
lr_decay = [0.001, 0.1, 0.5, 0.99]
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for decay, ind in zip(lr_decay, plt_ind):
plt.subplot(ind)
learn_rate = np.exp(-epochs * decay)
plt.plot(epochs, learn_rate, c='cyan')
plt.title('decay rate: ' + str(decay))
plt.xlabel('epochs $t$')
plt.ylabel('$eta^(t)$')
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()

Функція віддалі до найближчого сусіда
Дано:
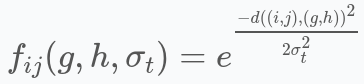
де ( d((i,j),(g,h)) ) — це відстань координат (i,j) клітинки від координат BMU (g,h), а ( σ_{t} ) — радіус в epoch t. Як правило, евклідова відстань використовується для обчислення дистанції, однак, можна використовувати будь-яку іншу віддаль або показник подібності.
Оскільки віддаль BMU до себе самої дорівнює нулю, зміна ваги BMU скорочується до:
[ Δw_{gh} = η(x−w_{gh}) ]
Для одиниці (i, j), що має значну віддаль від BMU, функція віддалі до найближчого сусіда зменшується до майже нульового значення та зменшення величини ( Δw_{ij} ). Отже, на такі одиниці не впливає навчальний приклад x. Один навчальний приклад впливає лише на BMU та клітинки безпосередньо біля BMU. Колими віддаляємось від BMU, зміна ваги стає дедалі меншою, поки не стане зовсім незначною.
Радіус визначає зону впливу тренувального прикладу x. Вище значення радіусу впливає на більшу кількість клітин, а менший радіус впливає лише на BMU. Загальна стратегія: почати з великого радіуса і зменшити його протягом періоду, тобто:
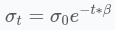
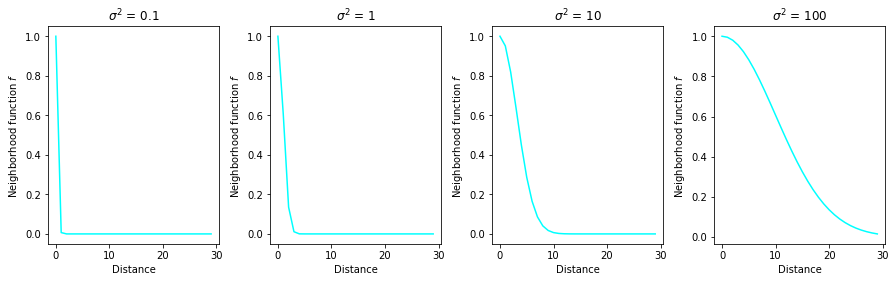
Маємо β < 0 — швидкість спадання. Вона відповідає радіусу і впливає на радіус так само, як і швидкість спадання, що відповідає швидкості навчання. Щоб отримати глибше уявлення про поведінку функції найближчого сусіда, побудуймо графік залежності, щоб визначати відстані для різних значень радіуса. Слід зазначити, що на цих графіках функція відстані наближається до майже нульового значення, коли відстань перевищує 10 для ( σ^{2} ≤ 10 ).
Пізніше ми використаємо цей факт, щоб зробити навчання ефективнішим у частині імплементації:
distance = np.arange(0, 30)
sigma_sq = [0.1, 1, 10, 100]
fig,ax = plt.subplots(nrows=1, ncols=4, figsize=(15,4))
plt_ind = np.arange(4) + 141
for s, ind in zip(sigma_sq, plt_ind):
plt.subplot(ind)
f = np.exp(-distance ** 2 / 2 / s)
plt.plot(distance, f, c='cyan')
plt.title('$sigma^2$ = ' + str(s))
plt.xlabel('Distance')
plt.ylabel('Neighborhood function $f$')
fig.subplots_adjust(hspace=0.5, wspace=0.3)
plt.show()
Імплементація самоорганізованих карт у Python за допомогою NumPy
Оскільки немає вбудованого шаблону для SOM у де-факто стандартній бібліотеці машинного навчання Scikit-Learn, ми зробимо швидку реалізацію вручну за допомогою NumPy. Модель машинного навчання без нагляду досить проста і легко реалізовувана.
Ми імплементуємо SOM двовимірною сіткою mxn, що вимагає тривимірного масиву NumPy. Третій вимір потрібен для зберігання ваги у кожній клітинці:
# Повертаємо індекс (g,h) BMU до сітки
def find_BMU(SOM,x):
distSq = (np.square(SOM - x)).sum(axis=2)
return np.unravel_index(np.argmin(distSq, axis=None), distSq.shape)
# Оновлюємо вагу клітинок SOM при отриманні єдиного тренувального прикладу
# та параметрів моделі разом з координатами BMU як супроводу
def update_weights(SOM, train_ex, learn_rate, radius_sq,
BMU_coord, step=3):
g, h = BMU_coord
#якщо радіус близький до нуля, змінюється лише BMU
if radius_sq < 1e-3:
SOM[g,h,:] += learn_rate * (train_ex - SOM[g,h,:])
return SOM
# Змінюємо всі клітинки безпосередньо біля BMU
for i in range(max(0, g-step), min(SOM.shape[0], g+step)):
for j in range(max(0, h-step), min(SOM.shape[1], h+step)):
dist_sq = np.square(i - g) + np.square(j - h)
dist_func = np.exp(-dist_sq / 2 / radius_sq)
SOM[i,j,:] += learn_rate * dist_func * (train_ex - SOM[i,j,:])
return SOM
# Основна процедура підготовки SOM. Вимагає ініціалізованої сітки SOM
# або частково навченої сітки як параметра
def train_SOM(SOM, train_data, learn_rate = .1, radius_sq = 1,
lr_decay = .1, radius_decay = .1, epochs = 10):
learn_rate_0 = learn_rate
radius_0 = radius_sq
for epoch in np.arange(0, epochs):
rand.shuffle(train_data)
for train_ex in train_data:
g, h = find_BMU(SOM, train_ex)
SOM = update_weights(SOM, train_ex,
learn_rate, radius_sq, (g,h))
# Оновлюємо швидкість навчання та радіус
learn_rate = learn_rate_0 * np.exp(-epoch * lr_decay)
radius_sq = radius_0 * np.exp(-epoch * radius_decay)
return SOM
Розгляньмо ключові функції, що використовуються для імплементації самоорганізованої карти:
find_BMU() повертає координати клітинок сітки з найвідповіднішими модулями, якщо дано сітку SOM та навчальний приклад x. Він обчислює квадрат евклідової відстані між вагою кожної клітинки та x і повертає (g, h), тобто координати клітинки з мінімальною відстанню.
Для функції update_weights() потрібні сітка SOM, навчальний приклад X, параметри learn_rate and radius_sq, координати з найвідповіднішими модулями та параметр step. Теоретично, всі клітини SOM оновлюються у наступному тренувальному прикладі. Однак ми показали раніше, що зміна незначна для клітинок, які розташовані далеко від BMU. Отже, ми можемо зробити код ефективнішим, змінюючи лише клітинки поруч з BMU. Параметр step визначає максимальну кількість клітинок зліва, справа, вгорі та внизу, щоб змінити при оновленні ваги.
І, нарешті, функція train_SOM() реалізує основну процедуру підготовки SOM. Це вимагає ініціалізованої або частково підготовленої сітки SOM та train_data як параметрів. Перевагою повинна бути можливість тренувати SOM на попередній стадії тренування. Додатково необхідні параметри learn_rate та radius_sq разом з відповідною швидкістю спадання lr_decay та radius_decay. Параметр epochs типово має значення 10, але за потреби його можна змінити.
Приклад запуску самоорганізованих карт
Одним з найпопулярніших прикладів для навчання SOM — випадкові кольори. Ми можемо навчати SOM-сітку і легко візуалізувати, як різні подібні кольори розміщуються в сусідніх клітинках.
Клітинки, розташовані далеко одна від одної, мають різне забарвлення.
Запустімо функцію train_SOM() на навчальній матриці даних, заповненій випадковими кольорами RGB.
Наведений далі код ініціалізує тренувальну матрицю даних та SOM-сітку з випадковими кольорами RGB. Він також показує навчальні дані та ініціалізовану у випадковому порядку сітку SOM. Зауважте, тренажерна матриця — це матриця 3000x3, однак, ми перейшли до матриці 50x60x3 для візуалізації:
# Розміри сітки SOM
m = 10
n = 10
# Кількість навчальних прикладів
n_x = 3000
rand = np.random.RandomState(0)
# Ініціалізація навчальних даних
train_data = rand.randint(0, 255, (n_x, 3))
# Ініціалізація випадкового порядку SOM
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
# Показ навчальної матриці й сітки SOM
fig, ax = plt.subplots(
nrows=1, ncols=2, figsize=(12, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
ax[0].imshow(train_data.reshape(50, 60, 3))
ax[0].title.set_text('Training Data')
ax[1].imshow(SOM.astype(int))
ax[1].title.set_text('Randomly Initialized SOM Grid')

Тепер потренуймо SOM з перевіркою для кожних 5 повторень, щоб швидко побачити прогрес:
fig, ax = plt.subplots(
nrows=1, ncols=4, figsize=(15, 3.5),
subplot_kw=dict(xticks=[], yticks=[]))
total_epochs = 0
for epochs, i in zip([1, 4, 5, 10], range(0,4)):
total_epochs += epochs
SOM = train_SOM(SOM, train_data, epochs=epochs)
ax[i].imshow(SOM.astype(int))
ax[i].title.set_text('Epochs = ' + str(total_epochs))
self organizing map training and results

Наведений приклад дуже цікавий, оскільки він показує, як сітка автоматично розміщує кольори RGB, щоб різні відтінки одного кольору були поруч у сітці SOM. Упорядкування відбувається ще у першому періоді, але воно не ідеальне. Ми бачимо, що SOM збігається приблизно у 10 періодах і змін стає менше у наступних періодах.
Вплив швидкості навчання та радіусу
Щоб побачити залежність швидкості навчання для різних темпів навчання та радіусів, ми можемо запустити SOM для 10 періодів, починаючи з однакової початкової сітки. Код внизу тренує SOM для трьох різних значень швидкості навчання та трьох різних радіусів.
SOM відтворюється після 5 періодів для кожного моделювання:
fig, ax = plt.subplots(
nrows=3, ncols=3, figsize=(15, 15),
subplot_kw=dict(xticks=[], yticks=[]))
# Initialize the SOM randomly to the same state
for learn_rate, i in zip([0.001, 0.5, 0.99], [0, 1, 2]):
for radius_sq, j in zip([0.01, 1, 10], [0, 1, 2]):
rand = np.random.RandomState(0)
SOM = rand.randint(0, 255, (m, n, 3)).astype(float)
SOM = train_SOM(SOM, train_data, epochs = 5,
learn_rate = learn_rate,
radius_sq = radius_sq)
ax[i][j].imshow(SOM.astype(int))
ax[i][j].title.set_text('$eta$ = ' + str(learn_rate) +
', $sigma^2$ = ' + str(radius_sq))

Наведений приклад показує, що для значень радіусу, близьких до нуля (перший стовпець), SOM змінює лише окремі клітинки, але не сусідні клітинки. Отже, належна карта не створюється залежно від рівня навчання. Подібне трапляється і з меншими темпами навчання (перший рядок, другий стовпець). Як і для будь-якого іншого алгоритму машинного навчання, для ідеального результату потрібен хороший баланс параметрів.
Підсумок
У цій статті ми обговорили теоретичну модель SOM та її детальної реалізації. Продемонстрували SOM на кольорах RGB і показали, як різні відтінки однакового ж кольору організували себе на двовимірній сітці.
Хоча SOM вже не дуже популярні у спільноті машинного навчання, вони залишаються гарною моделлю для отримання підсумків та візуалізації даних.

Ще немає коментарів