До вашої уваги серія статей, де ми розглянемо, як застосовувати кілька моделей функціонального програмування, спростити програмування на JavaScript або, як у нашому випадку, підвищити швидкодію вашого коду.
У цій першій статті з серії ми розглянемо проблему швидкості виконання: як бути з повільними, тривалими функціями та як вдосконалити їх за допомогою мемоїзації. Це цікава методика, яка допомагає уникати зайвої роботи.
Спочатку ми розглянемо простий приклад з проблемами повільності, а потім подолаємо їх власноруч за допомогою цієї методики. Ми перейдемо до загального рішення, а завершимо оглядом мемоїзації у фреймворках та пришвидшенням роботи вебсторінок.
Приклад повільного коду
Поглянемо на простий, добре відомий приклад функції з серйозними проблемами швидкодії. У гнучких методологіях часто застосовується обчислення числа Фібоначчі (0, 1, 1, 2, 3, 5, 8, 13…), хоча інколи й з незначними змінами. Цей ряд починається з 0 та 1, а після цих двох перших значень наступні обчислюються як сума двох попередніх значень: 0+1=1, 1+1=2, 1+2=3, 2+3=5 і так до нескінченності. Тоді можна сказати, що fibo(0)=0, fibo(1)=1, а коли n більша за 1: fibo(n)=fibo(n‑2)+fibo(n‑1) — дуже просто!
Маленький відступ: Фібоначчі — це «Філіус Боначчі» або «син Боначчі». Фібоначчі також знаменитий тим, що приніс арабські цифри до Європи, замінивши громіздкі римські цифри. Його послідовність Фібоначчі випливає з розв'язку головоломки про кроликів, які розмножуються за такими ж простими правилами!
Ми можемо реалізувати це безпосередньо в JavaScript за допомогою рекурсії.
const fibo = (n) => {
if (n === 0) {
return 0;
} else if (n === 1) {
return 1;
} else /* n > 1 */ {
return fibo(n - 2) + fibo(n - 1);
}
};
Функція працює правильно, все чудово і мило… хіба що код досить повільний! Ця функція обробляє багато значень n, створюючи цілу плеяду цих значень. На діаграмі показано експоненційне зростання значень простого обчислення, яке повинно мати лише кілька сум… що це нам дає?
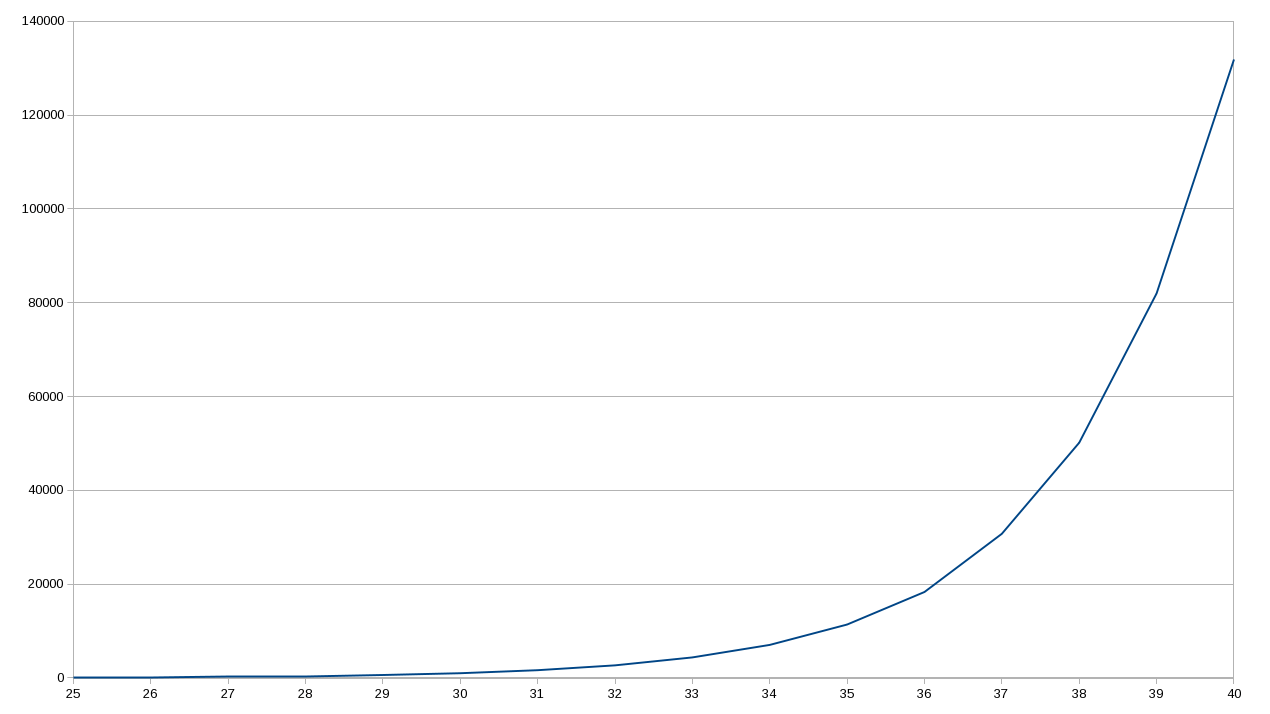
Щоб зрозуміти першопричину цих затримок, просто зобразимо виклики під час обчислення fibo(6). Зображення далі допомагає побачити основну проблему… занадто багато повторних, непотрібних викликів функції!
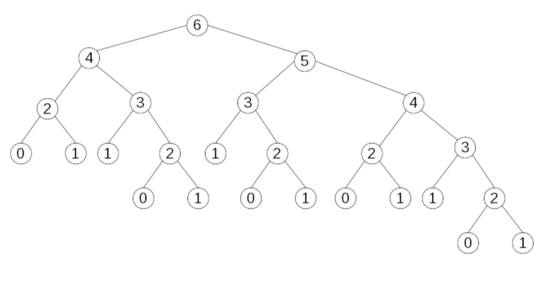
Ми можемо перевірити: є один виклик для fibo(6), чудово, один для fibo(5) — теж чудово, але fibo(4) викликається двічі, fibo(3) тричі, і їхня кількість зростає для решти fibo(2), fibo(1) та fibo(0).
Скільки викликів потрібно для обчислення fibo(n)? Назвемо їх calls(n), calls(0)=calls(1)=1 (непотрібна рекурсія). Якщо n>1, calls(n)= 1+calls(n‑2)+calls(n‑1): виклик fibo(n) плюс виклик для fibo(n‑2) та fibo(n‑1). Послідовність буде 1, 1, 3, 5, 9, 15, 25 (виклики для fibo(6); перевірте це!), 41, 67, 109 і до нескінченності. Ці числа називаються числами Леонардо, але назва здається походить від імені Фібоначчі (Леонардо Боначчі), а не від Леонардо да Вінчі.
Отже, зрозуміло, що наш рекурсивний метод марнує багато часу, щоб повторно виконати дії, які вже виконувалися… Як можна цього уникнути?
Часткове розв'язання
Проблема, яку ми намагаємось розв'язати, досить поширена; наприклад, у динамічному програмуванні (техніка оптимізації для певних класів проблем) ми також отримуємо повторні виклики (як у нашому прикладі Фібоначчі), які повторно виконують раніше зроблену роботу. Ми можемо пропустити ці повторні виклики, переписавши частини нашого коду, зробивши нашу функцію складнішою і працюючи з кешем.
const already_calculated = {};
const fibo = (n) => {
if (!(n in already_calculated)) {
if (n === 0) {
already_calculated[0] = 0;
} else if (n === 1) {
already_calculated[1] = 1;
} else /* n > 1 */ {
already_calculated[n] = fibo(n - 2) + fibo(n - 1);
}
}
return already_calculated[n];
};
Ми застосуємо об'єкт (already_calculated) як кеш. За кожного виклику fibo(n) ми спочатку перевіряємо, чи вже проводили це обчислення, і дивимось, чи є n у нашому кеші. Якщо ні, виконується обчислення, і поміщаємо його в кеш. Результат завжди повертається з кешу: return already_calculated[n].
Це працює (спробуйте!) і швидкодія чудова, адже якщо є якісь повторні рекурсивні виклики, вони підсумовуються і ми отримуємо необхідне значення з кешу. Але не все так сонячно у данському королівстві:
- Ми повинні використовувати глобальний об'єкт кешу (
already_calculated), але глобальні змінні — це погана практика. - Нам довелося змінити код нашої функції, щоб використовувати кеш, а зміна коду завжди може спричинити помилки.
- Ми не можемо масштабувати код: якщо нам доведеться оптимізувати кілька функцій, то знадобиться більше глобальних змінних та більше змін у коді.
Як бачимо, задум працює, але нам потрібне універсальніше розв'язання, бажано без перерахованих недоліків. Відповідь — мемоїзація, техніка функціонального програмування.
Універсальніше розв'язання
Нам потрібно знайти спосіб уникати повторення тривалих, повільних обчислень, виконаних раніше. Мемоїзація — це загальна техніка функціонального програмування, яку ви можете застосувати до будь-якої чистої функції. Тобто функції без будь-яких додаткових властивостей, яка завжди дає однаковий результат, якщо викликається з однаковими аргументами.
Мемоїзація створює нову функцію, яка буде внутрішньо перевіряти кеш раніше обчислених значень. Якщо там знайдено необхідний результат, він повернеться без будь-яких подальших дій. Якщо значення в кеші немає, всі необхідні дії буде виконано, але до запиту результат зберігатиметься в кеші (що ми робили власноруч у попередньому розділі), тому він буде доступний для майбутніх викликів.
Оскільки ми не хочемо змінювати наш початковий код, ми хочемо записати функцію memoize(...), яка прийматиме будь-яку загальну функцію аргументом і створюватиме нову, яка працюватиме так само як і оригінальна функція, але з застосуванням кешування, щоб уникнути повторного виконання. Ми можемо записати цю функцію так:
const memoize = (fn) => {
const cache = new Map(); /* (1) */
return (n) => {
if (!cache.has(n)) { /* (2) */
cache.set(n, fn(n)); /* (3) */
}
return cache.get(n); /* (4) */
};
};
Наша функція memoize(...) є функцією вищого порядку, тому що вона отримує функцію своїм параметром і повертає нову функцію у вигляді результату; це поширений шаблон для функціонального програмування.
Як виглядає повернена функція? Асоціативний масив (map) cache визначено в (1) — і застосування JavaScript Map доцільніше, ніж використання об'єкта асоціативним масивом (map), — і значення змінної cache буде об'єднано разом із поверненим результатом функції за допомогою замикання; тут не потрібно ніяких глобальних змінних! Нова функція починається з перевірки (2), чи є вже у кеші необхідний результат; якщо ні, ми робимо обчислення (3) і переносимо результат у кеш. У всіх випадках повернене значення (4) надходить безпосередньо з кешу. Блискуче!
Можемо перевірити це досить просто; напишемо таке:
const fibo = memoize((n) => {
if (n === 0) {
return 0;
} else if (n === 1) {
return 1;
} else {
return fibo(n - 2) + fibo(n - 1);
}
});
Зауважте, що це той самий код, що й раніше, з єдиною відмінністю, де ми додавали тіло функції fibo() з викликом до memoize(). Якщо перевіряти цю функцію, незалежно від того, яке значення n ви впишете, швидкодія буде високою, а fibo(n) повертатиметься дуже швидко. Однак наш розв'язок має вади… Що робити, якщо наша початкова проблемна функція очікує два або три аргументи, а не один? Варто вдосконалити наш код.
По-справжньому універсальне розв'язання
Попередній варіант був недостатньо універсальним; що робити з функціями з двома або більше параметрами? Фокус полягає у перетворенні аргументів функції у рядок, який ми можемо застосовувати ключем для нашого асоціативного масиву (map). Це легко зробити за допомогою JSON.stringify, і наша нова версія memoize(...) буде такою:
const memoize = (fn) => {
const cache = new Map();
return (...args) => {
const strX = JSON.stringify(args);
if (!cache.has(strX)) {
cache.set(strX, fn(...args));
}
return cache.get(strX);
};
};
Це досить універсально і ми можемо застосовувати такий спосіб для всіх функцій, незалежно від кількості очікуваних параметрів. Це працюватиме навіть з функціями зі змінною кількістю параметрів; розумієте чому? Наша функція мемоїзації є досить ефективною, але якщо вам потрібна мемоїзація у вашому коді, краще робити це за допомогою fast-memoize, яка може похвалитися найшвидшим із доступних мемоїзаторів.
Ми розглянули проблему швидкодії й два її розв'язання: звичайне та універсальне… Але перш ніж розібрати, як працювати з мемоїзацією в деяких фреймворках для написання вебінтерфейсів, подивімось на можливі вади.
Ледь помітна помилка!
Ви можете подивитись на код з попереднього розділу і здивуватись: чому ж було не написати такий код, щоб уникнути модифікації визначення fibo(n)?
const betterFibo = memoize(fibo);
У цьому і полягає непомітність помилки, але спершу гляньмо на це в дії! По-перше, деякі виклики надсилаються оригінальній не мемоїзованій функції fibo(). (не взято до уваги кілька вимірювань; ви побачите, чому це зайве). Час виконання був приблизно таким, як наведено далі. Зауважте, що fibo(45) обчислювався двічі… і явно (ну, приблизно) виконувалося той же час; безумовно, час завантаження на нашому комп'ютері дещо різнився між експериментами, але це не важливо.
| n | fibo(n) |
|---|---|
| 45 | 17644 мс |
| 45 | 17652 мс |
| 40 | 1602 мс |
| 35 | 135 мс |
| 30 | 12 мс |
| 25 | 1 мс |
Повторивши тести з функцією мемоїзації fibo(n), ми побачимо очікуване і значне пришвидшення. Перше обчислення тривало лише 7 мс, а всі інші виконувалися майже миттєво, оскільки всі необхідні значення були попередньо обчислені для знаходження fibo(45). Чудово, все як і планувалось!
| n | мемоїзований fibo(n) |
|---|---|
| 45 | 7 мс |
| 45 | 1 мс |
| 40 | 1 мс |
| 35 | 1 мс |
| 30 | 1 мс |
| 25 | 1 мс |
Тепер повторимо тести, але з betterFibo(n). З'являються несподівані результати! Перший виклик триває так само довго, як оригінальна функція fibo(n)? Повторний виклик для betterFibo(45) досить швидкий, значить він застосовує кешоване значення… але всі інші виклики знову сповільнені?
| n | betterFibo(n) |
|---|---|
| 45 | 17692 мс |
| 45 | 1 мс |
| 40 | 1749 мс |
| 35 | 186 мс |
| 30 | 16 мс |
| 25 | 1 мс |
Проблема важлива, а її можна легко не помітити. Ключовим є те, що betterFibo(n) всередині себе викликає оригінальну функцію fibo(n), а не мемоїзовану. Результат для betterFibo(45) справді кешується (оптимізований 2-й рядок у нашій таблиці), але всі інші виклики fibo(n) не кешуються, і логічно, що швидкодія така ж низька, як раніше.
Що могло б спрацювати, це написання чогось схожого на цей код, але зауважте, що ми не застосовували const у визначенні fibo(n).
let fibo = (n) => {
if (n === 0) {
return 0;
} else if (n === 1) {
return 1;
} else /* n > 1 */ {
return fibo(n - 2) + fibo(n - 1);
}
};
fibo = memoize(fibo);
Інший спосіб, який міг би спрацювати — це визначення fibo(n) класичним способом, без стрілкової функції.
function fibo2(n) {
if (n === 0) {
return 0;
} else if (n === 1) {
return 1;
} /* n > 1 */ else {
return fibo2(n - 2) + fibo2(n - 1);
}
}
fibo2 = memoize(fibo2);
Функція fibo2(n) працює ідеально, оскільки в JavaScript ви можете перепризначити функцію. Однак, якщо ви користуєтеся ESLint, ви отримаєте заперечення, тому що функції перепризначення часто є джерелом помилок, а правило no-func-assign забороняє його.
Мемоїзація чи кешування?
Ви повинні бути обережними, читаючи про «кешування» або «мемоїзацію» в документації для таких фреймворків, як Vue або React, оскільки вона може робити не те, що ви очікуєте. Наприклад, у Vue ви обчислили властивості, а їхня документація говорить, що «обчислені властивості кешуються на основі їхніх реактивних залежностей [і] переобчислюватимуться лише тоді, коли деякі його реактивні залежності змінюються». Схоже згадується у документації для getter для обчислених значень у Vuex: «результат геттера кешується на основі його залежностей і переобчислюватиметься, лише якщо деякі його залежності змінилися».
В обох випадках йдеться не про мемоїзацію: а лише про те, що Vue досить розумний, аби не повторювати обчислення для вже обчисленого значення, якщо жодна з його залежностей не змінилася. Якщо обчислене значення залежить від атрибутів X, Y та Z, Vue не буде повторно виконувати обчислення значення, якщо не зміниться X, Y або Z; водночас він кешує раніше обчислене значення.
Схожа проблема є й у React. Хук useMemo() «переобчислює мемоїзоване значення, лише якщо одна з залежностей змінилася» — по суті те саме, що робить Vue, але це теж не мемоїзування; він просто пам'ятає одне попереднє обчислення. Знову ж, useCallback() оперує таким самим типом обмеженого кешування, і це зрозуміло, оскільки useCallback(fn, dependencies) еквівалентно useMemo(()=>fn, dependencies). Зрештою, React.memo(...) аналогічно робить спрощену оптимізацію за допомогою кешування, просто уникаючи перемальовування компонента, якщо його властивості ті ж, що й під час останнього виклику. Але й він не виконує повноцінну мемоїзацію, а лише кешує попередній результат.
Підсумуємо
У цій статті ми розглянули кілька підходів до мемоїзації і як з її допомогою можна прискорити виконання вашого коду. Однак не думайте, що мемоїзація є «універсальним солдатом» для всіх проблем швидкості; інколи вона може навіть поглибити проблеми! Зауважте, що мемоїзація передбачає дві додаткові витрати ресурсів: вам потрібна додаткова кеш-пам'ять для всіх вже обчислених значень, а ще — додатковий час, щоб перевірити та застосувати сам кеш. Якщо ви працюєте з функцією, яка рідко (або й ніколи) викликається з однаковими аргументами, мемоїзація вам не дуже допоможе і, мабуть, краще не застосовувати її. Як завжди, ви не повинні робити оптимізацію «на око»; спочатку все має бути виміряне!
Показаний тут розв'язок застосовується до загальних функцій. Але як щодо функцій, які роблять запити до API? Ви також можете застосовувати мемоїзцію для промісів — це оптимізує застосунок і дозволить скористатись іншими моделями, які пропонують реактивніший код. Тож до зустрічі у наступній статті!

Ще немає коментарів